minimind 学习笔记非常有用快速建立llm代码体系

#！1-如何从头训练tokenizer.md
# 一、导入训练tokenizer所需库

`tokenizers`是Hugging Face出的一个高性能、可定制的子词分词器库，主要用于训练和使用像BPE、WordPiece、Unigram等子词模型，是训练 LLM（如GPT/BERT）时常用的工具。

```python
 import random
import json
from tokenizers import (
    Tokenizer,
    decoders,
    models,
    pre_tokenizers,
    trainers,
)
import os
```

`Tokenizer`是核心分词器对象，控制整个分词、编码、解码过程，可以与不同的模型、预处理器和解码器配合使用。

`models`包含各种子词分词模型（如 BPE、WordPiece、Unigram），定义了如何对文本进行分割与映射成token IDs。

`pre_tokenizers`定义了文本的预处理方式，负责在真正的分词前对文本进行初步分割，如按空格、字节或其他规则分割。

`trainers`用于训练分词模型的工具，包括设置词表大小、特殊符号等的参数配置，常用的有 `BpeTrainer`、`WordPieceTrainer` 等。

`decoders`用于将分词后的 token IDs 转回原始文本（解码），支持不同的解码策略，如 `ByteLevel` 和 `Metaspace`。

# 二、初始化tokenizer

```python
tokenizer = Tokenizer(models.BPE())
tokenizer.pre_tokenizer = pre_tokenizers.ByteLevel(add_prefix_space=False)
```

代码首先定义了一个使用BPE模型的分词器，该分词器使用BPE算法将文本拆分成子词单元，以增强模型对未登录词和低频词的处理能力。

然后将预处理器设置为ByteLevel，这一步将文本转换为字节级别的单位，允许更细粒度的文本处理，且add_prefix_space=False控制是否在每个单词前加空格，由于处理的是中文，因此将其设置为False。

# 三、设置训练器trainer并添加特殊token

```python
# 定义特殊token
special_tokens = ["<|endoftext|>", "<|im_start|>", "<|im_end|>"]

# 设置训练器并添加特殊token
trainer = trainers.BpeTrainer(
    vocab_size=6400,
    special_tokens=special_tokens,  # 确保这三个token被包含
    show_progress=True,
    initial_alphabet=pre_tokenizers.ByteLevel.alphabet()
)
```

首先来看这些特殊tokens。

它们是在训练过程中专门定义的，用于标识特定的文本模式或结构，通常用于控制生成文本的结构。

* "<|endoftext|>"用于表示文本的结束，通常在模型生成任务中用来指示生成文本的终止。

* "<|im_start|>"标识对话或任务的开始，可以用于标记输入文本的起始。

* "<|im_end|>"标识对话或任务的结束，用来标记输入文本的结束。

这些特殊tokens会在训练过程中作为词表的一部分，确保它们在分词和生成过程中能被正确处理。

接下来解释trainer的参数。

* `vocab_size=6400`表示模型训练过程中会生成最多 6400 个子词（包括特殊 tokens）。一般情况下，词汇表的大小会在模型训练之前根据训练数据的大小和复杂度来决定。

* `special_tokens=special_tokens`用于标记特殊tokens，使得它们不会在BPE训练过程中被拆分或合并，因为这些特殊标记一般用于标记对话的开始或者结束等特殊意义，而没有明显的对话语义信息。具体来说，在 BPE 训练过程中，算法会找到文本中最频繁的字节对（或字符对），并将它们合并成新的词汇项。例如，BPE会将两个常见的字符组合，如'a'和'b'，合并成一个新的词汇项'ab'。然而，特殊tokens是不参与这一过程的。它们是已经定义好的、固定的标记，不会被拆分或进行BPE 合并。所以，当训练过程中遇到 "<|im_start|>" 这样的特殊token时，它会被保留为一个整体，BPE不会再进一步拆分它。

* `show_progress=True`用于在训练过程中会展示当前的训练进度，以便跟踪训练的进度和耗时。

* `initial_alphabet=pre_tokenizers.ByteLevel.alphabet()`指定了BPE模型的初始字母表。在这里使用的是ByteLevel的字母表，ByteLevel是一个字符级的预处理方法，它将文本拆解为字节级的子单元（包括字母、标点符号、空格等）。这一设置的作用是让训练器初始化时使用ByteLevel分词器的默认字母表，从而使得 ByteLevel分词器能够适应不同的字符和符号类型，特别是在处理包含非标准字符的文本时非常有用。

# 四、读取文本数据

使用预训练数据集训练tokenizer，为了便于演示，这里只读取前100条数据。

```python
# 读取JSONL文件并提取文本数据
def read_texts_from_jsonl(file_path, max_samples=100):
    with open(file_path, 'r', encoding='utf-8') as f:
        for i, line in enumerate(f):
            if i >= max_samples:
                break
            data = json.loads(line)
            yield data['text']

data_path = r'D:\MyFile\github\minimind-master\minimind_dataset\pretrain_hq.jsonl'
texts = read_texts_from_jsonl(data_path)
```

查看数据示例：

```python
print(list(texts)[1])
```

# 五、开始训练tokenizer

直接调用`tokenizer`的`train_from_iterator`方法即可开始训练

```python
# 训练tokenizer
tokenizer.train_from_iterator(texts, trainer=trainer)
```

# 六、设置解码器

为分词器设置一个 ByteLevel 解码器，让其在将 token ID 序列转换回原始文本时，能够正确还原被分词器按字节切分的内容。

```python
tokenizer.decoder = decoders.ByteLevel()
```

# 七、保存训练好的tokenizer

```python
tokenizer_dir = r"./model"
os.makedirs(tokenizer_dir, exist_ok=True)
tokenizer.save(os.path.join(tokenizer_dir, "tokenizer.json"))
tokenizer.model.save(tokenizer_dir)
```

# 八、手动创建并保存配置文件

```python
# 手动创建配置文件
config = {
    "add_bos_token": False,
    "add_eos_token": False,
    "add_prefix_space": False,
    "added_tokens_decoder": {
        "0": {
            "content": "<|endoftext|>",
            "lstrip": False,
            "normalized": False,
            "rstrip": False,
            "single_word": False,
            "special": True
        },
        "1": {
            "content": "<|im_start|>",
            "lstrip": False,
            "normalized": False,
            "rstrip": False,
            "single_word": False,
            "special": True
        },
        "2": {
            "content": "<|im_end|>",
            "lstrip": False,
            "normalized": False,
            "rstrip": False,
            "single_word": False,
            "special": True
        }
    },
    "additional_special_tokens": [],
    "bos_token": "<|im_start|>",
    "clean_up_tokenization_spaces": False,
    "eos_token": "<|im_end|>",
    "legacy": True,
    "model_max_length": 32768,
    "pad_token": "<|endoftext|>",
    "sp_model_kwargs": {},
    "spaces_between_special_tokens": False,
    "tokenizer_class": "PreTrainedTokenizerFast",
    "unk_token": "<|endoftext|>",
    "chat_template": "{% if messages[0]['role'] == 'system' %}{% set system_message = messages[0]['content'] %}{{ '<|im_start|>system\\n' + system_message + '<|im_end|>\\n' }}{% else %}{{ '<|im_start|>system\\nYou are a helpful assistant<|im_end|>\\n' }}{% endif %}{% for message in messages %}{% set content = message['content'] %}{% if message['role'] == 'user' %}{{ '<|im_start|>user\\n' + content + '<|im_end|>\\n<|im_start|>assistant\\n' }}{% elif message['role'] == 'assistant' %}{{ content + '<|im_end|>' + '\\n' }}{% endif %}{% endfor %}"
}

# 保存配置文件
with open(os.path.join(tokenizer_dir, "tokenizer_config.json"), "w", encoding="utf-8") as config_file:
    json.dump(config, config_file, ensure_ascii=False, indent=4)
```

| 字段名                          | 解释                                                         |
| ------------------------------- | ------------------------------------------------------------ |
| `add_bos_token`                 | 是否自动在文本开头添加 `bos_token`（如 `<|im_start|>`）。False 表示不添加。 |
| `add_eos_token`                 | 是否自动在文本末尾添加 `eos_token`（如 `<|im_end|>`）。False 表示不添加。 |
| `add_prefix_space`              | Byte-level 分词时是否在文本前加空格。通常英文中启用（True）更好，中文中设为 False。 |
| `added_tokens_decoder`          | 特殊 token 的详细配置。包括 token 内容、是否为特殊 token、是否仅限单词等。key 是内部 token ID。 |
| `additional_special_tokens`     | 除了 `bos/eos/pad/unk` 外，额外声明的特殊 token 列表。当前为空。 |
| `bos_token`                     | 起始 token，通常用于语言模型的开头控制符，这里设为 `<|im_start|>`。 |
| `clean_up_tokenization_spaces`  | 解码时是否清理 token 化带来的空格冗余。False 表示不清理。    |
| `eos_token`                     | 结束 token，通常用于语言模型输出结束的标记，这里设为 `<|im_end|>`。 |
| `legacy`                        | 设置为 `True` 兼容旧版本 `tokenizer` 行为。推荐保持默认。    |
| `model_max_length`              | 模型支持的最大 token 长度。超过将触发截断或报错。这里为 32768。 |
| `pad_token`                     | 用于对齐 padding 的特殊 token。此处为 `<|endoftext|>`。      |
| `sp_model_kwargs`               | SentencePiece 模型的额外配置参数（当前为 BPE，未使用，故为空）。 |
| `spaces_between_special_tokens` | 是否在特殊 token 之间自动添加空格。设置为 False。            |
| `tokenizer_class`               | 指定 tokenizer 类型。Hugging Face 使用 `"PreTrainedTokenizerFast"` 支持 Rust 实现加速。 |
| `unk_token`                     | 用于标记未知词（out-of-vocabulary）的 token，这里也设为 `<|endoftext|>`。 |
| `chat_template`                 | Jinja2 模板字符串，用于格式化对话数据为模型输入格式。适用于 Chat 模型（如 LLaMA2-Chat、ChatGPT）。 |

---

# 九、测试训练好的tokenizer

```python
def eval_tokenizer():
    from transformers import AutoTokenizer

# 加载预训练的tokenizer
    tokenizer = AutoTokenizer.from_pretrained(r"D:\MyFile\github\minimind-master\mm")

messages = [
        {"role": "system", "content": "你是一个优秀的聊天机器人，总是给我正确的回应！"},
        {"role": "user", "content": '你来自哪里？'},
        {"role": "assistant", "content": '我来自地球'}
    ]
    new_prompt = tokenizer.apply_chat_template(
        messages,
        tokenize=False
    )

# 获取实际词汇表长度（包括特殊符号）
    actual_vocab_size = len(tokenizer)
    print('tokenizer实际词表长度：', actual_vocab_size)

model_inputs = tokenizer(new_prompt)
    print('encoder长度：', len(model_inputs['input_ids']))

input_ids = model_inputs['input_ids']
    response = tokenizer.decode(input_ids, skip_special_tokens=False)
    print('decoder和原始文本是否一致：', response == new_prompt)

print('\n输入文本：\n',new_prompt,'\n')   
    print('解码文本：\n',response,'\n')

eval_tokenizer()
```

```
tokenizer实际词表长度： 259
encoder长度： 133
decoder和原始文本是否一致： True

至此，关于`minimind`中的tokenizer训练部分就解读完成了。
# 2. 
# 一、RMSNorm是什么

RMSNorm 是一种简单高效的 **归一化方法**，用于归一化神经网络中某一层的输出，使其数值保持稳定，常用于Transformer中。

给定输入向量x（x的shape为`[batch_size, seq_length, embedding_dim]`），RMSNorm 的计算方式为：

$$
\text{RMS}(x) = \sqrt{\frac{1}{d} \sum_{i=1}^{d} x_i^2 + \epsilon}
$$

$$
\text{RMSNorm}(x) = \frac{x}{\text{RMS}(x)} \cdot \gamma
$$

其中：

- $d$ 是token特征维度数
- $\epsilon$是防止除以零的小常数
- $\gamma$是可训练的缩放参数

```python
import torch
import torch.nn as nn

class RMSNorm(nn.Module):
    def __init__(self, dim: int, eps: float = 1e-5):
        super().__init__()
        self.eps = eps
        self.weight = nn.Parameter(torch.ones(dim))  # 可学习的缩放参数 γ
        # print(self.weight.shape)# torch.Size([4])

def _norm(self, x):
        # 均方根归一化：沿最后一维计算
        # torch.rsqrt返回的是x.pow(2).mean(-1, keepdim=True) + self.eps的平方根的倒数
        # 直接调用 rsqrt 比先 sqrt 再 1 / 更高效，尤其在 GPU 上
        return x * torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps)
    def forward(self, x):
        # print(self._norm(x.float()).shape)# # torch.Size([1, 2, 4])
        return self.weight * self._norm(x.float()).type_as(x)

# 实例化测试
x = torch.tensor([[[1.0, 2.0, 3.0, 4.0],
                   [5.0, 6.0, 7.0, 8.0]]])  # shape = (1, 2, 4)
norm = RMSNorm(dim=4)
output = norm(x)
print(output.shape)# torch.Size([1, 2, 4])
```

# 二、RMSNorm和LayerNorm的异同点

可以看到，RMSNorm和LayerNorm一样，归一化操作都是沿着每个token内部的特征维度（也就是输入x的embedding_dim维度）进行的，而不是沿着整个batch维度。这意味着它们对每个token都进行独立的标准化，而不是跨batch的归一化。

同时，相较于LayerNorm，RMSNorm不做 **减均值**的操作。这里把LayerNorm的计算公式和实现代码搬过来做一下对比：
$$
\text{LayerNorm}(\mathbf{x}) = \gamma \left( \frac{\mathbf{x} - \mu}{\sqrt{\sigma^2 + \epsilon}} \right) + \beta
$$

```python
class LayerNorm(nn.Module):
    def __init__(self, dim: int, eps: float = 1e-5):
        super().__init__()
        self.eps = eps
        self.weight = nn.Parameter(torch.ones(dim))  # γ
        self.bias = nn.Parameter(torch.zeros(dim))   # β

def forward(self, x):
        mean = x.mean(dim=-1, keepdim=True)            # 计算每个 token 的均值
        var = x.var(dim=-1, unbiased=False, keepdim=True)  # 方差
        x_norm = (x - mean) / torch.sqrt(var + self.eps)   # 标准化
        return self.weight * x_norm + self.bias

# 实例化测试
x = torch.tensor([[[1.0, 2.0, 3.0, 4.0],
                   [5.0, 6.0, 7.0, 8.0]]])  # shape = (1, 2, 4)
norm = LayerNorm(dim=4)
output = norm(x)
print(output.shape)# torch.Size([1, 2, 4])
```

可以看到，当均值为零时，LayerNorm就变成了RMSNorm。

# 三、为什么使用RMSNorm而不是LayerNorm？

RMSNorm的计算过程比LayerNorm更简单，因为它不涉及均值的计算，并且减少了一个可学习参数。LayerNorm在归一化时需要计算每个token的均值和方差，并使用它们来标准化输入。而RMSNorm只需要计算特征的平方和，减少了计算复杂度和内存消耗。

在处理大型模型时，输入的特征维度可能非常大，计算均值和方差的开销相对较大。RMSNorm去除了均值计算，因此可以节省计算资源，特别是在高维数据中，计算效率更高。

作者在各种场景中实验发现，使用RMSNorm能够减少约7%∼64%的计算时间。

# 四、引申：为什么RMSNorm和LayerNorm都在token特征维度上操作而非跨batch？

BatchNorm是在处理图像数据时常用的归一化方式。

图像数据通常有强烈的空间相关性，即相邻的像素通常会有相似的值或模式。因此，图像的像素特征在一个batch中通常有相似的分布，这使得在整个batch上做归一化是合理的。BatchNorm通过计算每个特征（比如每个通道）的均值和方差，能有效地减轻这些空间相关性带来的影响，并保证训练时每一层的输入保持一定的分布，从而加速收敛。

而在NLP任务中，每个token通常是一个具有特定语义和上下文信息的单位，比如每个token代表一个词。每个token的特征是通过模型的embedding层或Transformer层计算得到的，并包含了该token的语义信息。不同token的语义内容不同，所以它们的特征应该独立地进行归一化处理。

如果归一化操作发生在batch维度上，会导致不考虑每个token的独立性。用于归一化的数据来自不同的batch，包含不同的token内容和信息，如果跨batch进行标准化，会丢失token间的独立性，使得token之间存在耦合关系，比如一些padding token并没有实际意义，但是被加入了归一化计算，进而影响模型的学习效果。
# 3.
# 一、Sinusoidal PE是什么？

在Transformer原始论文《Attention is All You Need》中，作者使用了固定的**正余弦位置编码**Sinusoidal PE来为模型引入位置信息。其核心思想是利用不同频率的正弦波和余弦波对每个位置进行编码，具体公式如下：
$$
\text{PE}_{(pos, 2i)} = \sin\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right) \\
\text{PE}_{(pos, 2i+1)} = \cos\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right)
$$

其中，`pos`表示 token 在序列中的位置，取值范围为[0, 1, 2, ..., seq_len-1]；`i`表示embedding的维度索引，范围为$[0, 1, ..., d_{model}/2 - 1]$，`i`的所有取值总共有$d_{model}/2$个，每一个都分别通过施加sin或cos变换来对应某个token的embedding不同位置的偶数维与奇数维。

为了便于理解，这里来举个实际的例子来演示正余弦位置编码的工作原理。

假设$d_{model}$=8，token序列长度seq_len=120，现在需要计算序列中第2个位置（即`pos`=2）的token对应的位置编码，套公式：

计算每个维度的缩放因子：

| i    | 维度 (2i / 2i+1) | $\text{div\_term}_i = 10000^{2i/d_{\text{model}}}$ |
| ---- | ---------------- | -------------------------------------------------- |
| 0    | 0 / 1            | $10000^{0} = 1$                                    |
| 1    | 2 / 3            | $10000^{0.25} \approx 10$                          |
| 2    | 4 / 5            | $10000^{0.5} = 100$                                |
| 3    | 6 / 7            | $10000^{0.75} \approx 1000$                        |

带入公式计算 PE：

$$
\begin{aligned}
\text{PE}(2, 0) &= \sin(2/1) = \sin(2.0) \approx 0.9093 \\
\text{PE}(2, 1) &= \cos(2/1) = \cos(2.0) \approx -0.4161 \\
\text{PE}(2, 2) &= \sin(2/10) = \sin(0.2) \approx 0.1987 \\
\text{PE}(2, 3) &= \cos(2/10) = \cos(0.2) \approx 0.9801 \\
\text{PE}(2, 4) &= \sin(2/100) = \sin(0.02) \approx 0.0200 \\
\text{PE}(2, 5) &= \cos(2/100) = \cos(0.02) \approx 0.9998 \\
\text{PE}(2, 6) &= \sin(2/1000) = \sin(0.002) \approx 0.0020 \\
\text{PE}(2, 7) &= \cos(2/1000) = \cos(0.002) \approx 0.9999 \\
\end{aligned}
$$

---

最终位置编码向量（pos = 2）为：

[0.9093, -0.4161, 0.1987, 0.9801, 0.0200, 0.9998, 0.0020, 0.9999]

正余弦位置编码的代码实现如下：

```python
def sinusoidal_position_encoding(seq_len, d_model):
    """
    计算正余弦位置编码（Sinusoidal PE）。

参数：
    seq_len -- 序列长度
    d_model -- 模型的维度

返回：
    返回一个形状为 (seq_len, d_model) 的位置编码矩阵
    """
    # 创建位置编码矩阵
    position = np.arange(seq_len)[:, np.newaxis]  # shape为 (seq_len, 1)
    div_term = np.power(10000, (2 * (np.arange(d_model // 2)) / np.float32(d_model)))  # 频率缩放因子

# 计算正余弦位置编码
    pe = np.zeros((seq_len, d_model))
    pe[:, 0::2] = np.sin(position / div_term)  # 偶数维度用正弦
    pe[:, 1::2] = np.cos(position / div_term)  # 奇数维度用余弦

return pe

# 示例：计算 seq_len=120，d_model=8 的位置编码
seq_len = 120
d_model = 8
pe = sinusoidal_position_encoding(seq_len, d_model)

print(pe.shape)# (120, 8)
```

# 二、Sinusoidal PE的远程衰减特性

正余弦位置编码不需要学习参数，节省了计算资源和存储空间。两者的组合能够平滑过渡，适合建模序列中的位置关系，并捕捉token之间的相对位置差异。

正余弦位置编码具有远程衰减的特性：对于一个序列中每个token的向量，在对每个token施加RoPE时，从序列token视角来看，每个token向量的低维元素(i较小)在相邻token之间的变化比较快，而高维(i较大)则比较慢。

下面来推导一下这个结论，回看其数学计算公式:

$$
\text{PE}_{(pos, 2i)} = \sin\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right) \\
\text{PE}_{(pos, 2i+1)} = \cos\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right)
$$

可以发现，随着$i$ 增大（即embedding维度增大），每个维度的频率$\frac{pos}{10000^{2i/d_{\text{model}}}}$ 是减小的，导致位置编码在高维度下（即i较大）的变化变得缓慢。即，相邻位置的编码差异变得非常小，直到这些位置的编码几乎趋于相同。

同时，如果token序列长度非常长，随着`pos`值的增大，位置编码的变化变得越来越平缓，尤其是高维度的部分(即i较大)，位置之间的差异变得非常微小。

你可能会疑惑，`pos`值增大不是也可以使得频率项增大吗？注意这里指的是不同`pos`位置之间的差异会随着`pos`值的增大而减小，因为两个相邻`pos`位置的差异在分子上仅仅为1，而分母是指数级增长(2的幂次)！套入公式计算就可以看到，`i`和`pos`较大时两者的差异非常微小。

举个例子，假设$d_{\text{model}} = 512$，$i = 256$，所以分母为$\frac{1}{10000^1} = 10^{-4}$。考虑两个位置：pos = 1000 和 pos = 1001，计算两者编码差值：

$$
\Delta = \sin(10^{-4} \cdot 1001) - \sin(10^{-4} \cdot 1000)
$$

也就是：
$$
\Delta = \sin(0.1001) - \sin(0.1000) \approx 0.0998337 - 0.0998334 = 0.0000003
$$

结果差值极小，说明即使位置差异为 1，高维编码也几乎不变。

为了进一步验证这一点，这里绘制在不同的固定i取值下，pos的变化趋势：

```python
import numpy as np
import matplotlib.pyplot as plt

def sinusoidal_position_encoding(seq_len, d_model):
    """
    计算正余弦位置编码（Sinusoidal PE）。
    参数：
        seq_len -- 序列长度
        d_model -- 模型的维度
    返回：
        一个形状为 (seq_len, d_model) 的位置编码矩阵
    """
    position = np.arange(seq_len)[:, np.newaxis]  # (seq_len, 1)
    div_term = np.power(10000, (2 * (np.arange(d_model // 2)) / np.float32(d_model)))  # (d_model/2,)

pe = np.zeros((seq_len, d_model))
    pe[:, 0::2] = np.sin(position / div_term)  # 偶数维度使用正弦
    pe[:, 1::2] = np.cos(position / div_term)  # 奇数维度使用余弦

return pe

# 参数设置
seq_len = 512  # 序列长度
d_model = 128  # 模型的维度

# 获取位置编码
pe = sinusoidal_position_encoding(seq_len, d_model)

plt.figure(figsize=(10, 6))
fixed_pos = 10  # 固定位置
for i in [0,32,64]:  # 每6个维度展示一个
    plt.plot(np.arange(seq_len), pe[:, i], label=f'i={i}')
plt.xlabel("Position (pos)")
plt.ylabel("Position Encoding Value")
plt.title(f"Position Encoding at Fixed Position {fixed_pos} (Frequency Decrease with i)")
plt.legend(loc='upper right')
plt.tight_layout()
plt.show()
```

![](1.png)

x轴是不同的pos，y轴是相应pos下最终位置编码的元素值。可以看到，当i=0（较小）时，随着pos的增大，相邻pos之间的差异变化幅度较大，而随着i变大，比如i=64时，相邻pos之间的差异非常小。

如上图所示，当i=64（较大）时，即使pos从10增到20，y轴对应的值变化也不大，这种细微的变化难以被模型感知。也就是说，当序列变长（seq_length较大），远距离(较大的i)相邻token对应元素之间的差异会变得不明显。

# 三、Sinusoidal PE的缺陷

正余弦位置编码的最大缺陷在于，它只能提供绝对位置信息。在推理中，Attention模块计算的是Q和K的点积，而PE是直接加到embedding上，这使得**模型要学习如何将绝对位置转换为相对位置信息**，增加了学习负担。

同时，虽然它在理论上可以无限延伸到任意长度的序列，但在训练时只见过短序列，对应的PE向量是低频为主。当推理时输入超长句子（如 GPT-2训练长度为1024，推理输入4096），位置编码对应的频率极高，数值变化剧烈，模型之前没有见过这些位置模式，导致性能下降。

为了应对这些问题，旋转位置编码(RoPE)被提出。

RoPE继承了正余弦位置编码的远程衰减特性，但是通过将绝对位置编码转化为query和key的旋转操作，**将位置差异“嵌入”到注意力机制的点积中，转而感知token间的相对位置变化**。这一机制实质上**以绝对编码的形式实现了相对位置感知能力**，并保持了良好的可微性与推理效率，且通过周期性的旋转可以平滑外推到任意序列长度。

**一句话总结 RoPE 的本质贡献：**

> **RoPE以绝对位置编码的方式实现了相对位置编码，从而提升了Transformer模型对长序列中相对位置变化的敏感性和结构建模能力。**

在下一篇文章中，我们将详细讲解RoPE的内容，欢迎持续关注。
# 4.
正余弦位置编码的最大问题，在于它将绝对位置信息编码成固定的向量，然后通过加法加入token embedding。这种方式虽然能提供位置信息，但在注意力计算（q·k）中很容易被抵消，特别是高维度（较大的i）频率较低时，对短距离位置变化非常不敏感，导致模型在长序列任务中“分不清细节”。

为了解决这个问题，RoPE（Rotary Positional Embedding）通过一种旋转变换，**将位置信息直接融入到q和k的表示中**。

和正余弦编码一样，RoPE也没有引入需要学习的参数，但是RoPE将位置信息的引入方式从原来的“对于输入token的加法操作”变成了“对于q和k的旋转操作”，并且**以绝对位置编码的形式实现了相对位置编码**。

相对位置信息，即两个词向量(token embedding)之间的相对距离，假设在一个seq_length=100的序列中，两个词向量的位置pos分别为m和n，那它们之间的相对距离就是m-n，RoPE的目标就是在位置编码时引入m-n这一相对位置信息。

RoPE的目标，正是找到一种旋转操作，使得在不显式计算位置差m-n的情况下，位置编码自然地将“相对位置信息”融入到注意力机制中的$qk$中。换句话说，需要找到这么一种映射$g$，针对给定的两个用于计算注意力的向量$q$和$k$，以及m-n，使得
$$f(q,m)f(k,n)=g(q,k,m-n)$$

其中，$q$和$k$是长度为$d_{model}$的向量，m和n分别是对应向量中第m个和第n个pos处的元素。

参考：

https://zhuanlan.zhihu.com/p/667864459

https://kexue.fm/archives/8265/comment-page-2

# 一、回顾二维向量的旋转操作

根据线性代数的知识，二维向量的旋转操作，指的是对该二维向量施加一个旋转矩阵变换，变换前后只改变二维向量的方向而保持其模长不变。

给定一个二维向量：

$$
\mathbf{x} = \begin{bmatrix} x \\ y \end{bmatrix}
$$

我们希望将它在二维平面上**逆时针旋转**一个角度 $\theta$，可以通过乘以旋转矩阵来实现：

$$
\mathbf{x}_{\text{rot}} = R(\theta) \cdot \mathbf{x}
$$

其中旋转矩阵 $R(\theta)$ 为：

$$
R(\theta) = 
\begin{bmatrix}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{bmatrix}
$$

举个实际例子，若 $$\mathbf{x} = \begin{bmatrix} 1 \\ 0 \end{bmatrix}$$ 且 $$\theta = \frac{\pi}{2}$$

（即逆时针旋转 90°）：

$$
\mathbf{x}_{\text{rot}} = 
\begin{bmatrix}
\cos \frac{\pi}{2} & -\sin \frac{\pi}{2} \\
\sin \frac{\pi}{2} & \cos \frac{\pi}{2}
\end{bmatrix}
\begin{bmatrix}
1 \\
0
\end{bmatrix}
=
\begin{bmatrix}
0 \\
1
\end{bmatrix}
$$

即：向量从 $$(1, 0)$$ 旋转为 $$(0, 1)$$

用代码可视化上述旋转过程，如下：

```python
import numpy as np
import matplotlib.pyplot as plt

def rotate_2d(x, y, theta_rad):
    R = np.array([
        [np.cos(theta_rad), -np.sin(theta_rad)],
        [np.sin(theta_rad),  np.cos(theta_rad)]
    ])
    vec = np.array([x, y])
    return R @ vec

# 原始向量
x0, y0 = 1, 0

# 旋转角度（单位：弧度）
theta_deg = 90
theta_rad = np.deg2rad(theta_deg)

# 旋转后向量
x1, y1 = rotate_2d(x0, y0, theta_rad)

# 可视化
plt.figure(figsize=(6, 6))
plt.quiver(0, 0, x0, y0, angles='xy', scale_units='xy', scale=1, color='blue', label='original')
plt.quiver(0, 0, x1, y1, angles='xy', scale_units='xy', scale=1, color='red', label=f'rotate{theta_deg}° ')

# 坐标轴设置
plt.xlim(-1.5, 1.5)
plt.ylim(-1.5, 1.5)
plt.gca().set_aspect('equal')
plt.axhline(0, color='gray', linestyle='--', linewidth=0.5)
plt.axvline(0, color='gray', linestyle='--', linewidth=0.5)
plt.grid(True)
plt.legend()

plt.show()
```

![](1.png)

# 二、RoPE的工作原理（d_model=2）

前面说过，RoPE 是将位置信息通过旋转操作直接注入到注意力机制中的 $q$ 和 $k$ 向量中。

假设：

- 模型维度：$d_{\text{model}} = 2$

- 原始向量：
  $$
  \mathbf{q} = \begin{bmatrix} 1 \\ 2 \end{bmatrix}, \quad \mathbf{k} = \begin{bmatrix} 3 \\ 4 \end{bmatrix}
  $$

- 序列位置：设为 $\text{pos}_q = m$，$\text{pos}_k = n$

- 对应位置角频率为 $\theta = \omega \cdot \text{pos}$，其中 $\omega$ 是一个频率超参数

---

### Step 1: 对 q 和 k 分别旋转

定义二维旋转操作为：

$$
\text{RoPE}(\mathbf{x}, \theta) = 
\begin{bmatrix}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{bmatrix}
\cdot \mathbf{x}
$$

分别对 $\mathbf{q}$ 和 $\mathbf{k}$ 施加旋转：

- 设 $\theta_q = \omega \cdot m,\quad \theta_k = \omega \cdot n$
- 旋转后的向量为：

$$
\tilde{\mathbf{q}} = R(\theta_q)\cdot \mathbf{q}, \quad 
\tilde{\mathbf{k}} = R(\theta_k)\cdot \mathbf{k}
$$

---

### Step 2: 点积操作变成了**相对位置信息的函数**

旋转后计算注意力时，执行的是：

$$
\tilde{\mathbf{q}}^\top \cdot \tilde{\mathbf{k}} = \mathbf{q}^\top R(-\theta_q) R(\theta_k) \cdot \mathbf{k}
= \mathbf{q}^\top R(\theta_k - \theta_q) \cdot \mathbf{k}
$$

即：

> **RoPE 实现了 “绝对位置编码方式得到的相对位置感知”**：注意力变成了与 $(n - m)$（即位置差）相关的点积结果。

---

### 示例（假设 $\omega = 1$, $m = 1$, $n = 2$）

- 则 $\theta_q = 1$, $\theta_k = 2$
- $R(\theta_k - \theta_q) = R(1)$

那么有：

```python
import numpy as np

q = np.array([1, 2])
k = np.array([3, 4])

# 相对旋转角
theta = 1.0  # θ_k - θ_q
R = np.array([
    [np.cos(theta), -np.sin(theta)],
    [np.sin(theta),  np.cos(theta)],
])

k_rot = R @ k
att_score = q @ k_rot
print("注意力得分（RoPE）:", att_score)# 7.62626733416533，是一个数，代表了q向量中的第m个元素和k向量中的第n个元素的注意力得分。
```

事实上，RoPE将每对特征维度（比如 [x₀, x₁]）看作是二维平面上的一个点(x₀, x₁)，然后将其绕原点(0, 0)顺时针或逆时针旋转一个角度θ（由位置pos决定），这个操作的数学本质就是二维向量绕原点旋转。

这个旋转中心正是(0, 0)。所以可以想象：特征 [x0, x1] 像一个在平面上的箭头，RoPE 让它随着token的位置pos增大不断绕原点旋转，旋转角度=pos × freq_i。
![](D:\MyFile\github\minimind-master\notes\rope_rotation.gif)

# 三、推广到高维向量(词向量,d_model维,d_model >> 2)

上面介绍了当向量为二维时，RoPE的工作原理。

当向量维度非常高时，比如词向量的维度，可以**把高维向量中不同位置(i)的元素两两分成一组，分别执行旋转操作**，如下：

$$
\boldsymbol{R}_{\Theta,m}^{d_{model}} \boldsymbol{x} =
\begin{pmatrix}
\cos m\theta_0 & -\sin m\theta_0 & 0 & 0 & \cdots & 0 & 0 \\
\sin m\theta_0 & \cos m\theta_0 & 0 & 0 & \cdots & 0 & 0 \\
0 & 0 & \cos m\theta_2 & -\sin m\theta_2 & \cdots & 0 & 0 \\
0 & 0 & \sin m\theta_2 & \cos m\theta_2 & \cdots & 0 & 0 \\
\vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\
0 & 0 & 0 & 0 & \cdots & \cos m\theta_{d_{model}-2} & -\sin m\theta_{d_{model}-2} \\
0 & 0 & 0 & 0 & \cdots & \sin m\theta_{d_{model}-2} & \cos m\theta_{d_{model}-2}
\end{pmatrix}
\begin{pmatrix} 
x_0 \\
x_1 \\
x_2 \\
\vdots \\
x_{d_{model}-2} \\
x_{d_{model}-1}
\end{pmatrix}
$$

其中，$\Theta=\left\{\theta_i=\omega^{-\frac{i}{d_{model}}}, i \in [0, 2, \ldots, d_{model}-2] \right\}$。

注意，公式中的m指的是pos，即序列中第m个词向量的pos=m，之所以不用pos，是为了使得公式看起来简洁。

这个高维旋转矩阵是高度稀疏的，在代码实现时，通常改写成如下方式进行替代，以减少冗余计算：

$$
\boldsymbol{R}_{\Theta,m}^{d_{model}} \boldsymbol{x} = 
\begin{pmatrix}
x_{0} \\
x_{1} \\
x_{2} \\
x_{3} \\
\vdots \\
x_{d_{model}-2} \\
x_{d_{model}-1}
\end{pmatrix} 
\otimes 
\begin{pmatrix} 
\cos m\theta_0 \\
\cos m\theta_0 \\
\cos m\theta_2 \\
\cos m\theta_2 \\
\vdots \\
\cos m\theta_{d_{model}-2} \\
\cos m\theta_{d_{model}-2}
\end{pmatrix}
+ 
\begin{pmatrix}
-x_{1} \\
x_{0} \\
-x_{3} \\
x_{2} \\
\vdots \\
-x_{d_{model}-1} \\
x_{d_{model}-2}
\end{pmatrix} 
\otimes 
\begin{pmatrix} 
\sin m\theta_0 \\
\sin m\theta_0 \\
\sin m\theta_2 \\
\sin m\theta_2 \\
\vdots \\
\sin m\theta_{d_{model}-2} \\
\sin m\theta_{d_{model}-2}
\end{pmatrix}
$$

可以看到，经过RoPE，词向量的维度不变（仍为$d_{model}$）。

# 四、高维RoPE 示例：`d_model = 4`, `omiga = 10000`, `pos = 2`

假设原始向量（如query向量）为：

$$
\mathbf{q} = [1,\ 0,\ 0,\ 1]
$$

---

#### 第一步：计算频率

对于 $d_{model} = 4$，每2个维度一对：

$$
\text{freqs} = \left[ \frac{1}{10000^{0/4}},\ \frac{1}{10000^{2/4}} \right] = [1.0,\ 0.01]
$$

位置 $pos = 2$ 时，对应旋转角度为：

$$
\theta_0 = 2 \cdot 1.0 = 2.0 \\
\theta_1 = 2 \cdot 0.01 = 0.02
$$

---

#### 第二步：按维度对进行旋转

第1对维度 $(1,\ 0)$，角度 $2.0$：

$$
\begin{bmatrix}
\cos(2) & -\sin(2) \\
\sin(2) & \cos(2)
\end{bmatrix}
\cdot
\begin{bmatrix}
1 \\
0
\end{bmatrix}
=
\begin{bmatrix}
\cos(2) \\
\sin(2)
\end{bmatrix}
\approx
\begin{bmatrix}
-0.4161 \\
0.9093
\end{bmatrix}
$$

第2对维度 $(0,\ 1)$，角度 $0.02$：

$$
\begin{bmatrix}
\cos(0.02) & -\sin(0.02) \\
\sin(0.02) & \cos(0.02)
\end{bmatrix}
\cdot
\begin{bmatrix}
0 \\
1
\end{bmatrix}
=
\begin{bmatrix}
-\sin(0.02) \\
\cos(0.02)
\end{bmatrix}
\approx
\begin{bmatrix}
-0.02 \\
0.9998
\end{bmatrix}
$$

---

#### 第三步：RoPE 编码后向量

拼接两对旋转结果：

$$
\text{RoPE}(\mathbf{q}) = [-0.4161,\ 0.9093,\ -0.02,\ 0.9998]
$$

---

PyTorch 验证代码：

```python
import torch

d_model = 4
dd=d_model//2
omiga = 10000.0
m = 2

freqs = 1.0 / (omiga ** (torch.arange(0, d_model, 2).float() / d_model))
angles = m * freqs  # [2.0, 0.02]

q = torch.tensor([1.0, 0.0, 0.0, 1.0])

cos = torch.cat([torch.cos(angles), torch.cos(angles)])
sin = torch.cat([torch.sin(angles), torch.sin(angles)])

def rotate_half(x):
    return torch.cat([-x[dd:], x[:dd]])

q_embed = q * cos + rotate_half(q) * sin
print(q_embed)# tensor([-0.4161, -0.0200,  0.9093,  0.9998])，和手动计算的一致！
```

# 五、代码实现RoPE

https://zhuanlan.zhihu.com/p/645263524

在MiniMind中实现的RoPE参考了Transformers库的LLaMA模型中RoPE的实现方式，和上述公式有些区别，具体体现在：

假设输入高维向量为q=[1,2,3,4,5,6]

1. 应用上述公式做rotate_half(q)            --> [-2,  1, -4,  3, -6,  5]
2. 应用MiniMind/LLaMa的方法做rotate_half(q)      -->[-4, -5, -6,  1,  2,  3]

在这个链接中，证明了两者的等价性： https://discuss.huggingface.co/t/is-llama-rotary-embedding-implementation-correct/44509/2

这里我们展示MiniMind中的RoPE实现代码：

```python
def precompute_freqs_cis(d_model: int, end: int = int(32 * 1024), omiga: float = 1e6):
    freqs = 1.0 / (omiga ** (torch.arange(0, d_model, 2)[: (d_model // 2)].float() / d_model))
    t = torch.arange(end, device=freqs.device)# end是最长预计算freqs的长度，可任意扩增
    freqs = torch.outer(t, freqs).float()# 外积×：[end x 1, 1 x d_model//2)-->end x d_model//2 , 得到 "每个位置 × 每个频率" 的角度 θ
    freqs_cos = torch.cat([torch.cos(freqs), torch.cos(freqs)], dim=-1)# end x d_model//2--> end x d_model
    freqs_sin = torch.cat([torch.sin(freqs), torch.sin(freqs)], dim=-1)# end x d_model//2--> end x d_model
    return freqs_cos, freqs_sin

def apply_rotary_pos_emb(q, k, cos, sin, position_ids=None, unsqueeze_dim=1):
    def rotate_half(x):
        return torch.cat((-x[..., x.shape[-1] // 2:], x[..., : x.shape[-1] // 2]), dim=-1)

q_embed = (q * cos.unsqueeze(unsqueeze_dim)) + (rotate_half(q) * sin.unsqueeze(unsqueeze_dim))
    k_embed = (k * cos.unsqueeze(unsqueeze_dim)) + (rotate_half(k) * sin.unsqueeze(unsqueeze_dim))
    return q_embed, k_embed

d_model=4
q=torch.tensor([1,2,3,4])
k=torch.tensor([5,6,7,8])

freqs_cos, freqs_sin = precompute_freqs_cis(d_model)
q_embed, k_embed=apply_rotary_pos_emb(q,k,freqs_cos, freqs_sin)
print(q_embed.shape, k_embed.shape)# torch.Size([32768, 1, 4]) torch.Size([32768, 1, 4])   1是维度扩展得到的，4是d_model，32768是当前设置的最长序列长度
```
# 5.
MiniMind中的注意力机制包含了KV cache，GQA，Flash Attention等。

# 一、KV Cache

KV Cache（Key-Value Cache）是在Transformer自回归模型（如GPT）推理阶段中，为了加速推理、减少重复计算而引入的缓存机制。

具体来说，在推理时，为每个生成的token计算K和V矩阵，KV Cache将这些矩阵存储在内存中，以便在生成后续token时，我们只需为新的token计算K和V，而不是重新计算所有当前已生成token的K和V。

解码器以自回归的方式工作，如下面的GPT-2文本生成示例所示:

![](https://miro.medium.com/v2/resize:fit:720/format:webp/0*sexO6adGhaKr7aH0.gif)

在解码器的自回归生成中，给定一个输入，模型预测下一个token，然后在下一步将组合输入进行下一次预测。

这种自回归行为重复了一些操作，可以通过放大解码器中计算的掩码缩放点积注意力计算来更好地理解这一点：

![](https://miro.medium.com/v2/resize:fit:720/format:webp/1*8xqD4AYTwn6mQXNw0uhDCg.gif)

这里对是否使用KV Cache的QK计算过程进行对比：
![](https://miro.medium.com/v2/resize:fit:720/format:webp/1*uyuyOW1VBqmF5Gtv225XHQ.gif)

上图中，紫色是从缓存中获取的，绿色是计算得到的，灰色是根据causal机制（当前token只能看到自己以及之前的信息）被mask掉的（因此无需计算）。通过这些动图，可以很清晰的观察到使用KV Cache可以减少许多token的K和V向量的重复计算。

举个例子，假设在执行推理时，batch_size=1, 当前已经累计生成的toke数量为seq_len=511，hidden_size=512，num_query_heads = 8，num_key_value_heads = 2，

则head_dim = hidden_size / num_query_heads = 64，已经缓存的KV的shape均为[batch_size, seq_len,num_key_value_heads,head_dim] = [1,511,2,64]，并且将刚预测的新的token与已经预测的511个拼接在一起，总共512个，根据KV Cache的原理，在预测下一个token时，只需要计算新加入的第512个token（记作x）与所有512个token之间的注意力。

x 经过embedding层得到的shape为 [batch_size,seq_len,hidden_size]=[1,1,512]，然后通过线性层投影出xk和xv，shape都是 [batch_size,seq_len,num_key_value_heads*head_dim]=[1,1,2*64]，然后reshape成[batch_size,seq_len,num_key_value_heads,head_dim]=[1,1,2,64]，这就是最新生成的token的q和v，将其与缓存的前面512个token的q和v进行拼接，就得到了本次预测需要的KV矩阵，shape为concat([1,511,2,64],[1,1,2,64]) --> [1,512,2,64].

另外，这里快速介绍一下Transformer中的qkv，以加深理解：

在Transformer的翻译任务中，encoder接收[bsz,src_seq_len,hidden_size]的token embedding，经过attention等层输出[bsz,src_seq_len,hidden_size]作为kv(只生成一次)，供q多轮查询，q来自decoder，shape为[bsz,total_seq_len,hidden_size]，total_seq_len是decoder当前处理（已经生成）的序列长度。

# 二、MHA，MQA和GQA

在Transformer中，每一层的注意力通常是基于多头注意力（Multi-Head Attention, MHA）实现的。这个模块的核心操作是将模型的总隐藏维度$d_{model}$（MiniMind中也称之为hidden_dim）
拆分为多个“头”（heads），每个头独立地进行注意力计算，然后再将它们的结果拼接起来，投影回原始空间。

通过"多头"操作，每个头（head）可以专注不同的子空间，模型可以更好的捕捉多种不同的语义/结构关系。多个头并行，相当于多个子空间并行抽取特征，最后拼接后再映射，增强了模型的非线性表达能力。

既然"多头"操作有这些优势，那为什么还会出现GQA、MQA这种注意力机制呢？

实际上，MHA的并行多头机制虽然表达能力强，但它存在计算和内存上的开销问题。具体表现为：

* 在标准MHA中，每个头都需要独立的Q、K、V，共3个线性层，存储开销是成倍的。
* 在推理时，尤其是大模型部署中，每个token都要执行所有头的K/V计算并缓存，非常耗显存。

为了减少存储占用，出现了MQA，其核心思想是：每个注意力头依然保留独立的Query（Q）向量，但所有注意力头共享一组Key（K）和Value（V）向量。这样大大减少了计算和缓存中K/V的冗余部分。尤其在解码器结构中（如 GPT 系列），推理阶段需要缓存每个token的key/value，如果每个头都独立缓存，会造成巨大的显存压力，MQA 可以显著降低这种开销。

然而，由于K和V只有1个头，所有头的Q都共享这1个K和V，导致每个Query头无法获取独立的上下文信息，只能从同一组Key/Value中抽取信息。这在一定程度上限制了模型捕捉多样化注意力模式的能力，尤其是在建模复杂依赖关系或多语义对齐时可能效果不如标准MHA。

因此，虽然MQA在计算和显存占用方面具有显著优势，但也带来了表达能力的折损。这正是GQA出现的原因：通过让多个Q头共享部分（而不是全部）K/V子空间，GQA在保持效率的同时，部分恢复了MHA的灵活性和多样性，是一种性能与效率的折中设计。

这张图清晰的展示了MHA，MQA和GQA的区别：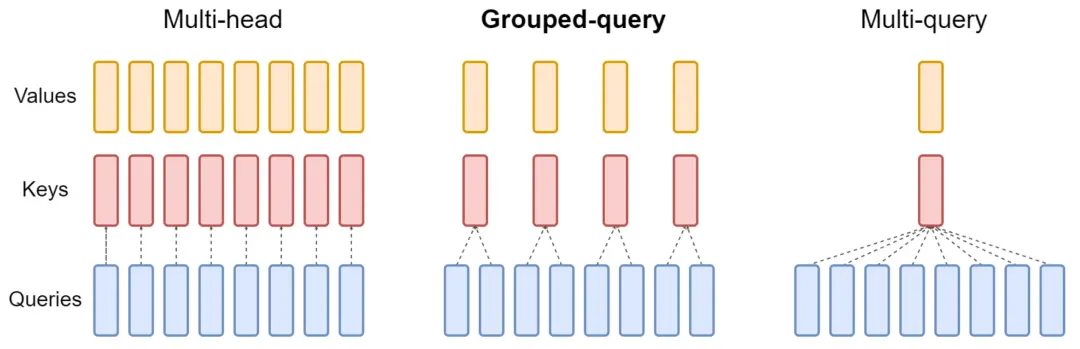

![](https://img-blog.csdnimg.cn/img_convert/2f6cbef83239dac5c58897d764a9dbb3.webp?x-oss-process=image/format,png)

注意，在计算注意力时，虽然MQA/GQA头数少，但通常会通过repeat/broadcast扩展回与Q相同的头数来做注意力计算，因此：从注意力矩阵计算（即 Q @ K^T 和 attention @ V）的FLOPs来上看，三者几乎是一样的。

但计算量不等于性能损耗，区别主要在：

* KV的投影次数（线性层）少了：MHA每头独立，KV线性投影各做num_heads次,MQA只做一次，GQA做M次（M是一个大于1 & 小于num_heads，且能够被num_heads整除的数）。这样一来， KV cache大幅减少，因为缓存的head 数是1或M，不是num_heads。
* KV的repeat操作可以高效实现：比如FlashAttention可以使用broadcast或index select避免真的物理复制(repeat)。

现在来举个例子，对比三者的存储开销，这里我们只比较注意力中K/V缓存的显存占用（推理时需保留），忽略 Q。

假设总隐藏维度$d_{model}$=4096，num_heads=32，seq_len=1024，batch_size=1，有head_dim=$d_{model}$//num_heads=4096//32=128，在GQA中将总共num_heads=32个Q向量分成8组。

每个float32占用4字节，每种方法的总存储占用（Byte）= `batch_size × num_kv_heads × seq_len × head_dim × float_size`

| 类型          | num_kv_heads | 计算公式                     | 显存占用（Byte） | 显存占用（MB） |
| ------------- | ------------ | ---------------------------- | ---------------- | -------------- |
| **MHA**       | 32           | 1×32×1024×128×4 = 16,777,216 | 16,777,216       | **16 MB**      |
| **GQA (8组)** | 8            | 1×8×1024×128×4 = 4,194,304   | 4,194,304        | **4 MB**       |
| **MQA**       | 1            | 1×1×1024×128×4 = 524,288     | 524,288          | **0.5 MB**     |

实际部署中，节省的是decoder每个token的KV缓存量，对于长序列推理影响显著。

如果真的希望减少计算量（而不仅仅是缓存量），就不能repeat kv，而是要修改attention的实现方式，让多个Q共享一个K/V。

# 三、Flash Attention

Flash Attention是一种**显存优化 + 更快计算**的注意力实现，数学本质不变，只是在实现细节上做了大量工程优化，尤其适用于长序列Transformer模型（如LLM）。

它通过采用流式分块计算，在softmax前后都不存中间结果，避免显存瓶颈。提供更高吞吐、更长上下文能力而不会爆显存。

在PyTorch中，可以简单的通过`torch.nn.functional.scaled_dot_product_attention`直接使用Flash Attention。

以上介绍的KV cache，GQA，Flash Attention均已在MiniMind的Attention模块进行了实现，如下：

```python
from typing import Optional, Tuple, List, Union
import torch.nn.functional as F

def repeat_kv(x: torch.Tensor, n_rep: int) -> torch.Tensor:
    """torch.repeat_interleave(x, dim=2, repeats=n_rep)"""
    bs, slen, num_key_value_heads, head_dim = x.shape
    if n_rep == 1:
        return x
    return (
        x[:, :, :, None, :]
        .expand(bs, slen, num_key_value_heads, n_rep, head_dim)
        .reshape(bs, slen, num_key_value_heads * n_rep, head_dim)
    )

class Attention(nn.Module):
    def __init__(self, args):
        super().__init__()
        # 支持多query-head共享同一个key/value-head
        self.num_key_value_heads = args.num_attention_heads if args.num_key_value_heads is None else args.num_key_value_heads
        assert args.num_attention_heads % self.num_key_value_heads == 0

self.n_local_heads = args.num_attention_heads  # 总的 attention head 数
        self.n_local_kv_heads = self.num_key_value_heads  # k/v head 数
        self.n_rep = self.n_local_heads // self.n_local_kv_heads  # 每个 k/v head 被多少个 query head 共享

self.head_dim = args.hidden_size // args.num_attention_heads  # 每个 head 的维度

# QKV线性映射层，不使用 bias
        self.q_proj = nn.Linear(args.hidden_size, args.num_attention_heads * self.head_dim, bias=False)
        self.k_proj = nn.Linear(args.hidden_size, self.num_key_value_heads * self.head_dim, bias=False)
        self.v_proj = nn.Linear(args.hidden_size, self.num_key_value_heads * self.head_dim, bias=False)
        self.o_proj = nn.Linear(args.num_attention_heads * self.head_dim, args.hidden_size, bias=False)

# dropout
        self.attn_dropout = nn.Dropout(args.dropout)
        self.resid_dropout = nn.Dropout(args.dropout)
        self.dropout = args.dropout

# 是否启用 Flash Attention（PyTorch >= 2.0）
        self.flash = hasattr(torch.nn.functional, 'scaled_dot_product_attention') and args.flash_attn

def forward(self,
                x: torch.Tensor,  # 输入特征: [bsz, seq_len, hidden_size]
                position_embeddings: Tuple[torch.Tensor, torch.Tensor],  # rotary pos embedding 的 cos/sin
                past_key_value: Optional[Tuple[torch.Tensor, torch.Tensor]] = None,  # kv缓存
                use_cache=False,  # 是否返回 kv_cache
                attention_mask: Optional[torch.Tensor] = None):  # attention 掩码（padding的token不参与注意力计算）

bsz, seq_len, _ = x.shape

# 线性变换 -> Q, K, V
        xq = self.q_proj(x)  # [bsz, seq_len, n_heads * head_dim]
        xk = self.k_proj(x)  # [bsz, seq_len, n_kv_heads * head_dim]
        xv = self.v_proj(x)  # [bsz, seq_len, n_kv_heads * head_dim]

# reshape 为多头格式
        xq = xq.view(bsz, seq_len, self.n_local_heads, self.head_dim)
        xk = xk.view(bsz, seq_len, self.n_local_kv_heads, self.head_dim)
        xv = xv.view(bsz, seq_len, self.n_local_kv_heads, self.head_dim)

# 应用 rotary position embedding
        cos, sin = position_embeddings
        # cos和sin是预计算的很长的一段，这里只截取前seq_len，因为最大pos就是seq_len-1
        xq, xk = apply_rotary_pos_emb(xq, xk, cos[:seq_len], sin[:seq_len])

# 处理 KV 缓存：将历史的 key/value 与当前拼接(训练时不需要)
        if past_key_value is not None:
            xk = torch.cat([past_key_value[0], xk], dim=1)  # time 维度拼接
            xv = torch.cat([past_key_value[1], xv], dim=1)

past_kv = (xk, xv) if use_cache else None # xk/xv：[bsz, seq_len, self.n_local_kv_heads, self.head_dim]

# KV head 重复扩展 -> 让所有 Q head 对应到正确的 KV head
        xq = xq.transpose(1, 2)  # [bsz, n_heads, seq_len, head_dim]
        xk = repeat_kv(xk, self.n_rep).transpose(1, 2)  # [bsz, n_heads, seq_len, head_dim]
        xv = repeat_kv(xv, self.n_rep).transpose(1, 2)  # [bsz, n_heads, seq_len, head_dim]

# Flash Attention 方法（更快更省内存）
        if self.flash and seq_len != 1:
            dropout_p = self.dropout if self.training else 0.0
            attn_mask = None
            if attention_mask is not None:
                attn_mask = attention_mask.view(bsz, 1, 1, -1).expand(bsz, self.n_local_heads, seq_len, -1)
                attn_mask = attn_mask.bool()

# 使用 PyTorch 原生 flash attention（内置 causal）
            output = F.scaled_dot_product_attention(
                xq, xk, xv,
                attn_mask=attn_mask,
                dropout_p=dropout_p,
                is_causal=True
            )

# 普通 attention 方法
        else:
            # 注意力分数计算
            scores = (xq @ xk.transpose(-2, -1)) / math.sqrt(self.head_dim)  # [bsz, n_heads, q_len, k_len]

# 添加上三角 mask，实现 causal attention
            scores = scores + torch.triu(
                torch.full((seq_len, seq_len), float("-inf"), device=scores.device),
                diagonal=1
            ).unsqueeze(0).unsqueeze(0) # scores+mask， 上三角变成-inf，经过softmax后趋于0，从而遮盖未来信息

# attention 掩码（如 padding mask）
            if attention_mask is not None:
                extended_attention_mask = attention_mask.unsqueeze(1).unsqueeze(2)  # [bsz,seq_len]-->[bsz,1,1,seq_len]
                extended_attention_mask = (1.0 - extended_attention_mask) * -1e9 # 需要掩的位置是0，现在变成了-1e9，非常小
                scores = scores + extended_attention_mask # 掩的位置后面经过softmax就近似为0了

# softmax + dropout
            scores = F.softmax(scores.float(), dim=-1).type_as(xq)
            scores = self.attn_dropout(scores)

# 注意力加权求和
            output = scores @ xv  # [bsz, n_heads, q_len, head_dim]

# 还原输出形状，并通过输出线性层
        output = output.transpose(1, 2).reshape(bsz, seq_len, -1)
        output = self.resid_dropout(self.o_proj(output))

return output, past_kv
```

这里涉及到3个mask，其作用分别为：

* 屏蔽未来信息：torch.triu(torch.full((seq_len, seq_len), float("-inf"), device=scores.device),diagonal=1).unsqueeze(0).unsqueeze(0)
* padding的token不参与注意力计算：attention_mask，shape是[batch_size,seq_len]。在MiniMind训练时，默认是None，可根据实际情况进行调整。
* 训练时，padding的token不参与loss计算：loss = (loss * loss_mask).sum() / loss_mask.sum() [这个来自训练代码]

参考：

- [1] https://medium.com/@joaolages/kv-caching-explained-276520203249

- [2] https://neptune.ai/blog/transformers-key-value-caching
# 6.
# 一、稠密模型中的FFN

稠密模型（Dense Model）是指模型结构中所有的参数和计算路径在每次前向计算中都会被激活，与下一小节要介绍的稀疏模型MoE形成对比。

相比于原始Transformer中使用的FFN，这里的FFN引入了Gated结构，可以动态地控制信息流通（比如抑制/强调特定特征），增加了表达能力。目前很多SOTA模型（如 LLaMA、PaLM、GPT-NeoX、ChatGLM）都不再用原始 FFN，而是使用带门控机制（Gated）的前馈神经网络FFN。

这里对两者进行对比：

| 特性       | 标准 FFN    | 增强版 FFN（Gated）    |
| ---------- | ----------- | ---------------------- |
| 激活函数   | ReLU / GELU | GELU / SiLU / Swish 等 |
| 中间结构   | 单路计算    | 双路计算（乘积）       |
| 参数量     | 较少        | 多一个 Linear 层       |
| 非线性能力 | 一般        | 更强（引入乘法门控）   |
| 性能表现   | 基线        | 表现更好（SOTA 标配）  |

增强版FFN的代码实现如下：

```python
# 激活函数映射字典
ACT2FN = {
    "relu": F.relu,
    "gelu": F.gelu,
    "silu": F.silu
}

class FeedForward(nn.Module):
    def __init__(self, config: dict):
        super().__init__()
        if config["intermediate_size"] is None:
            intermediate_size = int(config["hidden_size"] * 8 / 3)
            # 为了更好地利用 GPU 的并行计算能力（特别是 TensorCore、SIMD 等），中间维度通常会做 64 对齐
            # 向上取整到最近的 64 的倍数
            config["intermediate_size"] = 64 * ((intermediate_size + 64 - 1) // 64)

self.gate_proj = nn.Linear(config["hidden_size"], config["intermediate_size"], bias=False)
        self.down_proj = nn.Linear(config["intermediate_size"], config["hidden_size"], bias=False)
        self.up_proj = nn.Linear(config["hidden_size"], config["intermediate_size"], bias=False)
        self.dropout = nn.Dropout(config["dropout"])
        self.act_fn = ACT2FN[config["hidden_act"]]

def forward(self, x):
        return self.dropout(
            self.down_proj(self.act_fn(self.gate_proj(x)) * self.up_proj(x))
        )

# 示例配置
config = {
    "hidden_size": 512,
    "intermediate_size": None,  # 自动计算
    "dropout": 0.1,
    "hidden_act": "silu"  # 也可以试试 "gelu", "relu"
}

# 创建模型和输入
ffn = FeedForward(config)
x = torch.randn(2, 16, 512)  # (batch_size, seq_len, hidden_size)

# 前向传播
out = ffn(x)
print("Output shape:", out.shape) # Output shape: torch.Size([2, 16, 512])
```

这里的“门控机制”具体的逻辑是这样的：

首先，通过 gate = act_fn(gate_proj(x)) 得到门控信号（范围通常为[0, 1]或正数）；

其次，通过 value = up_proj(x) 得到要被控制的信息通道；

接着，使用 gated = gate * value 应用门控，控制信息强度（本质上就是加权）；

最后，使用output = down_proj(gated) 降维回去，门控完成。

# 二、稀疏模型MoE

## 2.1 MOE的工作原理

稠密模型适合中小规模模型结构，部署和训练更简单稳定，是大多数基础模型（如GPT、BERT、LLaMA）的核心形式。

但如果想让模型变得更大、更强，而又不想付出巨额推理开销，可以使用稀疏模型（比如MoE），这是一种更具扩展性的结构。其核心思想是：模型参数很多，但每次只激活其中一部分（部分专家），通过门控（Gating）机制选择专家进行预测、最后组合专家输出。

参考：

https://medium.com/@drahyhenc/mixture-of-experts%E5%AD%B8%E7%BF%92%E7%AD%86%E8%A8%98-80fae09a1b5e

在MiniMind中，MOE主要应用在Attention之后的FFN上。

原始的FFN使用的是我们上面定义的一个FeedForward类，而MOE的思想是将“原始FFN中只包含一个FeedForward”替换成“FFN中包含多个FeedForward”，其中每一个FeedForward都是一个专家，这乍看上去增加了很多参数，但是在实际的数据流动时，只会选择其中top-k个专家，也就是只会激活top-k个FeedForward，从而节省计算时间（但是还是需要将所有专家都加载到显存的，不省显存省时间，应对策略是把模型放在主内存里，需要的时候把相应的专家模型加载到显卡上进行推理）。

注意，在训练时，每一个专家都会被更新参数，训练完成后，“不同的专家擅长不同领域知识”这一目标就达成了，每个专家都得到了训练。在数据流向MOE时，会根据“学习到的经验”选择合适的专家进行处理。

现将MOE的执行流程总结为如下四步：

第一步、对每个 token，使用 MoEGate 打分，选择 top-k 个专家（例如 k=2）

第二步、只将 token 输入给这 k 个专家（repeat_interleave）

第三步、每个专家输出后加权求和（使用 gate 输出的 softmax 权重）

第四步、返回合并后的输出

![](https://miro.medium.com/v2/resize:fit:1400/format:webp/1*pAeeowS0tdDy4YZH751icA.png)

相应的MOE主体实现代码如下：

```python
class MOEFeedForward(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.config = config

# 初始化专家网络（仅路由专家）
        self.experts = nn.ModuleList([
            FeedForward(config)
            for _ in range(config.n_routed_experts)
        ])

# 初始化门控网络
        self.gate = MoEGate(config) # MoEGate 将在下一小节介绍

# 可选：共享专家网络（作用于每个 token）
        if config.n_shared_experts > 0:
            self.shared_experts = nn.ModuleList([
                FeedForward(config)
                for _ in range(config.n_shared_experts)
            ])

def forward(self, x):
        """
        x: [bsz, seq_len, hidden_size]
        """
        identity = x  # 用于 residual 加上共享专家输出
        orig_shape = x.shape
        bsz, seq_len, _ = x.shape  # bsz = batch size, seq_len = token 数量

# ===== 1. 门控阶段：选择 top-k 个专家 作为每个 token 的路由 =====
        topk_idx, topk_weight, aux_loss = self.gate(x)
        # topk_idx:    [bsz * seq_len, top_k]
        # topk_weight: [bsz * seq_len, top_k]

# ===== 2. Flatten token 维度，准备并行处理 token =====
        x = x.view(-1, x.shape[-1])
        # x: [bsz * seq_len, hidden_size]

flat_topk_idx = topk_idx.view(-1)
        # flat_topk_idx: [(bsz * seq_len) * top_k]，表示每个 token 被分配到的专家 ID

if self.training:
            # ===== 3. 训练阶段：每个 token 被复制 top_k 次，送入不同专家 =====
            x = x.repeat_interleave(self.config.num_experts_per_tok, dim=0)
            # x: [(bsz * seq_len) * top_k, hidden_size]

# 用于收集每个专家处理后的结果
            y = torch.empty_like(x, dtype=torch.float16)

# 遍历每个专家，将其处理分配给它的 token
            for i, expert in enumerate(self.experts):
                # 找出所有分配给第 i 个专家的 token
                mask = (flat_topk_idx == i)
                x_i = x[mask]  # [num_token_i, hidden_size]

if x_i.shape[0] > 0:
                    y[mask] = expert(x_i).to(y.dtype)  # expert 输出: [num_token_i, hidden_size]

# 恢复 top_k 维度，并根据 gate 分数加权平均
            y = y.view(*topk_weight.shape, -1)  # [bsz * seq_len, top_k, hidden_size]
            y = (y * topk_weight.unsqueeze(-1)).sum(dim=1)# 在 top_k 维度进行了加权求和
            # y: [bsz * seq_len, hidden_size]

# reshape 回原始形状
            y = y.view(*orig_shape)  # [bsz, seq_len, hidden_size]

else:
            # ===== 4. 推理阶段：使用高效推理模式（按专家分组处理） =====
            topk_weight = topk_weight.view(-1, 1) # [bsz * seq_len, top_k] --> [bsz * seq_len * top_k, 1]
            y = self.moe_infer(x, flat_topk_idx, topk_weight)
            y = y.view(*orig_shape)  # [bsz, seq_len, hidden_size]

# ===== 5. 加上共享专家的输出（可选）=====
        if self.config.n_shared_experts > 0:
            for expert in self.shared_experts:
                y = y + expert(identity)  # 每个共享专家都作用在原始输入上并加到输出上

self.aux_loss = aux_loss  # 保存门控产生的辅助损失
        return y
    
    @torch.no_grad()
    def moe_infer(self, x, flat_expert_indices, flat_expert_weights):
        """
        推理阶段的 MoE 前向传播。按照专家编号将 token 分组，分别送入对应专家中计算后合并。
        
        参数：
        - x: [bsz * seq_len, hidden_size]             所有 token 的表示（没有复制）
        - flat_expert_indices: [(bsz * seq_len) * top_k]  每个 token 被路由到的专家编号
        - flat_expert_weights: [(bsz * seq_len) * top_k , 1] 每个专家对应的门控权重
        """

# 初始化输出缓存，与 x 同 shape 和 dtype
        expert_cache = torch.zeros_like(x)  # shape: [bsz * seq_len, hidden_size]

# 1. 根据专家编号对所有 token 排序（为了把分配到相同专家的 token 放到一起）
        idxs = flat_expert_indices.argsort()  # 按照专家索引从小到大排序后得到 专家分组排序后token（复制了top_k倍）的索引， 这是一个列表

# 2. 统计每个专家分配到的 token 数量并累加，方便切分
        tokens_per_expert = flat_expert_indices.bincount().cpu().numpy().cumsum(0)
        # tokens_per_expert[i] 表示第 i 个专家前面（由其它专家）累积处理了多少个 token

# 3. 计算按照专家分组排序后的 token 属于哪些原始 token（因为每个 token 会被复制 top_k 次）
        token_idxs = idxs // self.config.num_experts_per_tok
        # shape: [(bsz * seq_len) * top_k]

# 4. 遍历每个专家，将分配到该专家的 token 送入对应 FFN 计算
            # 当tokens_per_expert = [6, 15, 20, 26]，tokens_per_expert.shape[0]即为专家数量（此时为4）
            # 且token_idxs = [3, 7, 19, 21, 24, 25,  4,  5,  6, 10, 11, 12...] 时
            # 意味token_idxs[:6] -> [3, 7, 19, 21, 24, 25]这6个位置属于专家0处理的token（每个token有可能被多个专家处理，这取决于num_experts_per_tok）
            # 接下来9个位置token_idxs[6:15] -> [4,  5,  6, 10, 11, 12...]属于专家1处理的token...依此类推
        for i, end_idx in enumerate(tokens_per_expert):
            start_idx = 0 if i == 0 else tokens_per_expert[i - 1]
            if start_idx == end_idx:
                continue  # 该专家没有被分配 token
            # 上述 start_idx ~ end_idx 是某一个专家i需要负责处理的token数量

expert = self.experts[i]  # 获取专家 FFN 模块

# 5. 获取分配给第 i 个专家的 token 原始位置索引
            # 即：expert_out 中每一行对应的是原始输入中哪个 token。
            exp_token_idx = token_idxs[start_idx:end_idx]  # [num_token_i]

# 6. 取出对应 token 表示
            expert_tokens = x[exp_token_idx]  # [num_token_i, hidden_size]

# 7. 执行当前专家对应 FFN 的前向传播
            expert_out = expert(expert_tokens).to(expert_cache.dtype)  # [num_token_i, hidden_size]

# 8. 用 gate 权重缩放输出
            # expert_out.mul_(...)  等价于 expert_out = expert_out * ...
            # [num_token_i, hidden_size] * [num_token_i, 1] --> [num_token_i, hidden_size]
            expert_out.mul_(flat_expert_weights[idxs[start_idx:end_idx]])  # 权重 shape: [num_token_i, 1]

# 9. 累加到输出缓存中，支持一个 token 被多个专家处理后结果叠加
            expert_cache.scatter_add_(
                dim=0,
                # [num_token_i] -->  [num_token_i, 1] --> [num_token_i, hidden_size]
                index=exp_token_idx.view(-1, 1).repeat(1, x.shape[-1]), 
                # [num_token_i, hidden_size]
                src=expert_out 
            )

# 最终输出 shape: [bsz * seq_len, hidden_size]
        return expert_cache
```

在上述代码中，MiniMind实现的MOE代码中还加入了共享的专家，这些专家都作用在原始输入上并加到输出上。

同时，针对推理场景，上述代码实现了高效地将 token 分派给不同专家并进行前向计算、加权输出、聚合结果等操作。其核心思想是：**按照专家(0, 1, 2, ...)对复制top_k倍的所有token索引进行分组排序。**

为了便于理解推理过程，这里举一个具体的例子。

假设我们有以下配置：

假设有以下配置：

```python
bsz = 2             # batch size
seq_len = 2         # 每个样本 2 个 token
hidden_size = 4     # 每个 token 的向量维度
top_k = 2           # 每个 token 路由到 top_k 个专家
num_experts = 3     # 总共 3 个专家
```

也就是说：

* 总 token 数 = bsz * seq_len = 4
* 每个 token 分给 2 个专家，共 8 个分配记录
* x.shape = [4, 4]（4 个 token，每个是 4 维）

第一步、准备输入数据：

```python
x = torch.tensor([
    [0.1, 0.2, 0.3, 0.4],  # token 0
    [1.0, 1.1, 1.2, 1.3],  # token 1
    [2.0, 2.1, 2.2, 2.3],  # token 2
    [3.0, 3.1, 3.2, 3.3],  # token 3
])  # shape: [4, 4]
```

第二步、top-k 专家分配（假设已经由 gate 模块得出）：

```python
flat_expert_indices = torch.tensor([
    0, 1,   # token 0 → expert 0, 1
    1, 2,   # token 1 → expert 1, 2
    0, 2,   # token 2 → expert 0, 2
    0, 1    # token 3 → expert 0, 1
])  # shape: [8]

# flat_expert_indices的含义是：
# 第0个token被分配给专家0（flat_expert_indices[0]）
# 第0个token被分配给专家1（flat_expert_indices[1]）
# 第1个token被分配给专家1（flat_expert_indices[2]）
# 第1个token被分配给专家2（flat_expert_indices[3]）
# 第2个token被分配给专家0（flat_expert_indices[4]）
# 第2个token被分配给专家2（flat_expert_indices[5]）
# 第3个token被分配给专家0（flat_expert_indices[6]）
# 第3个token被分配给专家1（flat_expert_indices[7]）

# 也就是说，共有 4 个 token，每个 token 被复制分配了 2 次 → 长度 8。

flat_expert_weights = torch.tensor([
    [0.9], [0.1],   # token 0
    [0.3], [0.7],   # token 1
    [0.4], [0.6],   # token 2
    [0.5], [0.5],   # token 3
])  # shape: [8, 1]

# flat_expert_weights 是对应的权重
```

第三步、推理阶段关键逻辑：

* Step 1: idxs = flat_expert_indices.argsort()

```python
flat_expert_indices = [0, 1, 1, 2, 0, 2, 0, 1]
idxs = flat_expert_indices.argsort()
# 即：让所有 token 的分配记录按专家编号排好序

# flat_expert_indices = [0, 1, 1, 2, 0, 2, 0, 1]
# 对应排序后：
# expert 0 负责: index 0, 4, 6
# expert 1 负责: index 1, 2, 7
# expert 2 负责: index 3, 5

# 所以 按专家编号分组排序后的索引是：
idxs = [0, 4, 6, 1, 2, 7, 3, 5]

# 这些索引是token（复制top_k倍后）的索引
```

* Step 2: token_idxs = idxs // top_k

```python
idxs = [0, 4, 6, 1, 2, 7, 3, 5]
top_k = 2
token_idxs = = idxs // top_k = [0, 2, 3, 0, 1, 3, 1, 2]
# 意思是这些位置的 token index（被专家处理的）：
# token idx=0 → 原始 token 0
# token idx=4 → 原始 token 2
# token idx=6 → 原始 token 3
# ...
```

因为 flat_expert_indices 是对 token 被复制分配之后的顺序排列，我们知道每个原始 token 复制了 top_k=2 次，所以：

| 位置（flat\_expert\_indices的索引） | 对应原始token |
| ----------------------------------- | ------------- |
| 0, 1                                | token 0       |
| 2, 3                                | token 1       |
| 4, 5                                | token 2       |
| 6, 7                                | token 3       |

所以只要对 token index 整除 top_k 就能还原它是哪个 token。

* Step 3: tokens_per_expert = flat_expert_indices.bincount().cpu().numpy().cumsum(0)

```python
flat_expert_indices = [0, 1, 1, 2, 0, 2, 0, 1]
# 每个专家被多少 token 分配到（按复制计算）：
# expert 0 → 3 次，expert 1 → 3 次，expert 2 → 2 次
tokens_per_expert = [3, 6, 8]  # 前缀和：分割 token 的分配区间
```

Step 4: 依次送入每个专家处理：

Expert 0：

```
分配到 idxs[0:3] = [0, 4, 6]
对应 token_idxs = [0, 2, 3] → 原始 token 的 index
从 x 取出 x[0], x[2], x[3] → 做前向
输出乘上 gate 权重 [0.9], [0.4], [0.5]
加到 expert_cache 的位置 0, 2, 3
```

Expert 1：

```
idxs[3:6] = [1, 2, 7]
token_idxs = [0, 1, 2]
取出 x[0], x[1], x[2]
输出乘上 [0.1], [0.3], [0.5]
累加到 expert_cache 的位置 0, 1, 2
```

Expert 2：

```
idxs[6:8] = [3, 5]
token_idxs = [1, 3]
取出 x[1], x[3]
输出乘上 [0.7], [0.6]
累加到 expert_cache 的位置 1, 3
```

expert_cache最终就是所有专家处理过的结果的加权累加和，每个token位置被多个专家处理，最后叠加权重输出。

最后，对训练和推理阶段的MOE执行过程做一个对比：

| 方面           | 训练阶段（Training）             | 推理阶段（Inference）           |
| -------------- | -------------------------------- | ------------------------------- |
| Token 是否复制 | 是，每个 token 被复制 `top_k` 次 | 否                              |
| 处理顺序       | 每个 token 独立送入专家          | 将所有 token 按专家分组批量处理 |
| 加权方式       | `top_k` 输出加权平均             | 用 `scatter_add_()` 加权累加    |
| 效率           | 低（但梯度计算方便）             | 高（节省内存，计算高效）        |
| 适用场景       | 训练                             | 推理（部署）                    |
| 多专家叠加     | 加权平均                         | 加权叠加                        |

## 2.2 MOE的负载均衡

https://ai.gopubby.com/deepseek-v3-explained-3-auxiliary-loss-free-load-balancing-4beeb734ab1f

https://www.linkedin.com/pulse/what-main-benefit-mixture-experts-moe-models-qi-he-nkgbe?utm_source=rss&utm_campaign=articles_sitemaps&utm_medium=google_news

在MOE_Gate打分的时候，可能偏向于给某几个专家打高分，导致token总是交给这几个专家处理，其余的专家总是处于空闲状态，这就是负载的不均衡，也称之为**路由坍塌(Route collapse)**。

路由坍塌的存在，会影响最终的模型效果。具体来说，由于过载的专家接收更多的输入token，它们也会积累更大的梯度，并且比负载较轻的专家学习得更快。结果，过载的专家和负载较轻的专家的梯度在幅度和方向上可能会发散，使得训练过程更难收敛。

为了实现专家的负载均衡，有许多不同的技术被提出来以处理这个问题。

### 2.2.1 专家选择(Expert Choice)

在原始的MOE中，是每个token给出对于所有专家的打分，然后每个token各自选出得分top_k大的top_k个专家，这是一个token选择专家的过程。负载不均衡指的就是某些专家一直没有被token选择。

Expert Choice将原先的“token选择专家”改成“专家选择要处理的token”：

![image.png](1.png)

每个专家都预先设置一个专家容量k，因此不会出现某些专家一直没有token可处理的情况。

然而，这种方法也有可能出现某些token使用了多个专家，而有些token只使用了很少甚至0个专家的情况。

### 2.2.2 辅助损失

在MiniMind源码中使用的是辅助损失的方式来应对路由坍塌问题。

在计算出每个token对于所有专家的打分后，每个token会选择top_k个得分高的专家进行后续处理。我们可以根据这里每个专家的得分（平均打分），以及每个专家实际被选中使用的频率（实际负载），来定义损失函数。具体来说，如果每个专家频繁被选中，并且每个专家的得分总是高于其它专家，那么就会惩罚这个专家。由于此时该专家对应的“平均打分 x 实际负载”比较高，将这个乘积作为一项loss进行惩罚。

基于这种思想，MiniMind分别从序列维度和整个batch维度进行了上述辅助损失函数的实现，相应的解释已经写在代码注释中，如下：

```python
class MoEGate(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.config = config
        self.top_k = config.num_experts_per_tok                    # 每个 token 分配的专家个数
        self.n_routed_experts = config.n_routed_experts           # 总可选专家数

self.scoring_func = config.scoring_func                   # 评分函数（仅支持 softmax）
        self.alpha = config.aux_loss_alpha                        # 辅助损失权重
        self.seq_aux = config.seq_aux                             # 是否使用序列级辅助损失

self.norm_topk_prob = config.norm_topk_prob               # 是否对 top-k 权重归一化
        self.gating_dim = config.hidden_size                      # gating 输入维度

self.weight = nn.Parameter(torch.empty((self.n_routed_experts, self.gating_dim)))  # [n_experts, hidden_dim]
        self.reset_parameters()

def reset_parameters(self) -> None:
        import torch.nn.init as init
        init.kaiming_uniform_(self.weight, a=math.sqrt(5))

def forward(self, hidden_states):
        """
        Args:
            hidden_states: [bsz, seq_len, hidden_dim]
        Returns:
            topk_idx: [bsz * seq_len, top_k] - top-k 专家索引
            topk_weight: [bsz * seq_len, top_k] - top-k 专家对应的权重
            aux_loss: scalar - 辅助损失，用于平衡专家负载
        """
        bsz, seq_len, h = hidden_states.shape
        hidden_states = hidden_states.view(-1, h)                     # [bsz * seq_len, hidden_dim]

logits = F.linear(hidden_states, self.weight, None)          # [bsz * seq_len, n_experts]

if self.scoring_func == 'softmax':
            scores = logits.softmax(dim=-1)                          # [bsz * seq_len, n_experts]
        else:
            raise NotImplementedError(f'insupportable scoring function for MoE gating: {self.scoring_func}')

topk_weight, topk_idx = torch.topk(scores, k=self.top_k, dim=-1, sorted=False)  # 都是 [bsz * seq_len, top_k]

if self.top_k > 1 and self.norm_topk_prob:
            denominator = topk_weight.sum(dim=-1, keepdim=True) + 1e-20
            topk_weight = topk_weight / denominator                  # [bsz * seq_len, top_k]
 
        # ========== Auxiliary Loss for Load Balancing ==========
        if self.training and self.alpha > 0.0:
            scores_for_aux = scores                                  # [bsz * seq_len, n_experts]
            aux_topk = self.top_k
            topk_idx_for_aux_loss = topk_idx.view(bsz, -1)           # [bsz, seq_len * top_k]

if self.seq_aux:  # 按 batch 维度分别计算每个样本内部的 expert 使用分布
                scores_for_seq_aux = scores_for_aux.view(bsz, seq_len, -1)   # [bsz, seq_len, n_experts]，按 batch 还原 gating scores

ce = torch.zeros(bsz, self.n_routed_experts, device=hidden_states.device)  # 初始化每个 batch 的 expert 统计图 [bsz, n_experts]

ce.scatter_add_(
                    dim = 1,
                    index = topk_idx_for_aux_loss,                           # [bsz, seq_len * top_k]，每个样本所有 token 的 top_k expert 索引
                    src = torch.ones(bsz, seq_len * aux_topk, device=hidden_states.device)  # [bsz, seq_len * top_k]，所有位置计数为1
                ).div_(seq_len * aux_topk / self.n_routed_experts)          # 标准化：理论上每个 expert 的理想负载是平均的 => 除以 (seq_len * top_k / n_experts)

# aux_loss 越大说明 score 分布与使用频率越不匹配（某些 expert 被打分高且被频繁使用）
                aux_loss = (ce * scores_for_seq_aux.mean(dim=1)).sum(dim=1).mean() * self.alpha  
                # - scores_for_seq_aux.mean(dim=1): [bsz, n_experts]，每个样本对每个 expert 的平均打分
                # - ce: 每个 expert 的归一化使用频率，越接近1说明越平均
                # - ce * score：频率高且分数高则惩罚高
                # - 最终 loss 对 batch 取平均，乘 alpha

else:
                mask_ce = F.one_hot(                      # one-hot 编码每个 token 被选中的 expert
                    topk_idx_for_aux_loss.view(-1),      # [bsz * seq_len * top_k]，flatten 后的所有 expert 索引
                    num_classes=self.n_routed_experts    # one-hot 中 expert 数量
                )  # => [bsz * seq_len * top_k, n_experts]

ce = mask_ce.float().mean(0)              # [n_experts]，每个 expert 被使用的频率（除以总 token 数量）

Pi = scores_for_aux.mean(0)               # [n_experts]，所有 token 对各 expert 的平均打分

fi = ce * self.n_routed_experts           # 频率 × expert 数 = 负载比，理想负载为1，偏离表示不均

aux_loss = (Pi * fi).sum() * self.alpha   # aux_loss = sum(Pi[i] * fi[i])，高打分 + 高负载的 expert 会被惩罚
                # - Pi: 平均打分，值越大说明 router 趋向于使用该 expert
                # - fi: 实际负载，值越大说明该 expert 被频繁使用
                # - Pi * fi：打分高且频率高的 expert 会导致更大的 loss（目标是让负载更均匀）

else:
            aux_loss = 0

return topk_idx, topk_weight, aux_loss
```

至此，MiniMind所涉及的组件就已经全部搭建完成了，在下一篇文章中，我们将这些组件组合起来，构建MiniMind网络，欢迎持续关注～
# 7.
现在已经完成了MiniMind中所有小组件的代码实现，将它们组合起来，就可以搭建MiniMind了。

这里展示的是MiniMind(Dense/MoE)的架构图
![](https://github.com/jingyaogong/minimind/raw/master/images/LLM-structure.png)
![](https://github.com/jingyaogong/minimind/raw/master/images/LLM-structure-moe.png)

首先来搭建一个用于构建MiniMind的基础模块`MiniMindBlock`，对应MiniMind架构图中的`Transformer Layer k`：

```python
class MiniMindBlock(nn.Module):
    def __init__(self, layer_id: int, config):
        super().__init__()
        # 基础配置
        self.num_attention_heads = config.num_attention_heads
        self.hidden_size = config.hidden_size
        self.head_dim = config.hidden_size // config.num_attention_heads

# 自注意力模块，内部实现了 RoPE 相对位置编码
        self.self_attn = Attention(config)

# 当前 Block 的层编号（可用于层内权重共享、分层控制等）
        self.layer_id = layer_id

# Attention 前的 RMSNorm
        self.input_layernorm = RMSNorm(config.hidden_size, eps=config.rms_norm_eps)

# Feed Forward 前的 RMSNorm
        self.post_attention_layernorm = RMSNorm(config.hidden_size, eps=config.rms_norm_eps)

# 前馈网络模块，可配置是否使用专家混合（MoE）
        self.mlp = FeedForward(config) if not config.use_moe else MOEFeedForward(config)

def forward(
        self,
        hidden_states,          # 输入的隐藏状态 [batch_size, seq_len, hidden_dim]
        position_embeddings,    # RoPE 位置编码 [seq_len, head_dim]
        past_key_value=None,    # KV 缓存 (key, value)，用于加速推理
        use_cache=False,        # 是否缓存当前层的 KV
        attention_mask=None     # attention 掩码
    ):
        # ---------------------- Self-Attention 层 ----------------------
        residual = hidden_states  # 保存残差连接

# 对输入做 RMSNorm，再送入自注意力层
        hidden_states, present_key_value = self.self_attn(
            self.input_layernorm(hidden_states),  # LayerNorm 后输入 attention
            position_embeddings,                 # Rotary PE 传入 Attention
            past_key_value,                      # 过往 KV 缓存（一般在推理阶段使用）
            use_cache,                           # 是否缓存当前层 KV（一般在推理阶段使用）
            attention_mask                       # 注意力掩码（padding token不计算注意力矩阵）
        )

# 残差连接：原始输入 + attention 输出
        hidden_states += residual

# ---------------------- MLP 层 ----------------------
        # MLP 前再做一次 RMSNorm
        normed_hidden = self.post_attention_layernorm(hidden_states)

# 残差连接：再加上 MLP 的输出
        hidden_states = hidden_states + self.mlp(normed_hidden)

# 返回新的 hidden_states 和 当前层的 KV 缓存
        return hidden_states, present_key_value
```

现在来搭建MiniMind：

```python
class MiniMindModel(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.config = config
        self.vocab_size, self.num_hidden_layers = config.vocab_size, config.num_hidden_layers

# [vocab_size, hidden_size] -> 用于将 token id 映射为向量
        self.embed_tokens = nn.Embedding(config.vocab_size, config.hidden_size)

self.dropout = nn.Dropout(config.dropout)

# 构建多个 Transformer Block 层
        self.layers = nn.ModuleList([
            MiniMindBlock(l, config) for l in range(self.num_hidden_layers)
        ])

# 输出前的 LayerNorm 层
        self.norm = RMSNorm(config.hidden_size, eps=config.rms_norm_eps)

# 预计算 RoPE 所需的位置频率向量 (cos/sin)
        freqs_cos, freqs_sin = precompute_freqs_cis(
            dim=config.hidden_size // config.num_attention_heads,
            end=config.max_position_embeddings,
            omiga=config.rope_theta
        )

# 注册为 buffer（模型中持久存储但不参与优化）
        self.register_buffer("freqs_cos", freqs_cos, persistent=False)  # [max_pos, head_dim]
        self.register_buffer("freqs_sin", freqs_sin, persistent=False)  # [max_pos, head_dim]

def forward(self,
                input_ids: Optional[torch.Tensor] = None,            # [B, T]
                attention_mask: Optional[torch.Tensor] = None,       # [B, 1, 1, T]（可选）
                past_key_values: Optional[List[Tuple[torch.Tensor, torch.Tensor]]] = None,  # 每层: [(B, S_cache, H_kv, D), (B, S_cache, H_kv, D)]
                use_cache: bool = False,
                **kwargs):

# B: batch_size, T: 当前输入 token 数量( T 在训练时就是seq_len，推理时就是当前已经生成的token数量)
        batch_size, seq_length = input_ids.shape  # [B, T]

# 如果没传入缓存，初始化为空（推理时才使用KV缓存）
        past_key_values = past_key_values or [None] * len(self.layers)

# 获取历史缓存长度（增量生成时使用）
        start_pos = past_key_values[0][0].shape[1] if past_key_values[0] is not None else 0

# 输入 ids -> 嵌入向量：[B, T] → [B, T, hidden_size]
        hidden_states = self.dropout(self.embed_tokens(input_ids))  # [B, T, H]

# 截取当前位置使用的旋转位置编码（RoPE）
        # freqs_cos: [max_pos, head_dim] → [T, head_dim]
        position_embeddings = (
            self.freqs_cos[start_pos:start_pos + seq_length],  # [T, D_head]
            self.freqs_sin[start_pos:start_pos + seq_length]   # [T, D_head]
        )

presents = []  # 存储 KV cache：每层一个 (key, value)

# 遍历每层 Transformer Block
        for layer_idx, (layer, past_key_value) in enumerate(zip(self.layers, past_key_values)):
            # 输入 hidden_states: [B, T, H]
            # 输出 hidden_states: [B, T, H]
            # 输出 present: (key, value)，用于缓存：[(B, T_total, H_kv, D), (B, T_total, H_kv, D)]
            hidden_states, present = layer(
                hidden_states,                # [B, T, H]
                position_embeddings,          # ([T, D_head], [T, D_head])
                past_key_value=past_key_value,
                use_cache=use_cache,
                attention_mask=attention_mask
            )
            presents.append(present)

# 最后输出 RMSNorm
        hidden_states = self.norm(hidden_states)  # [B, T, H]

# 如果使用了 MOE（稀疏专家），则合并辅助损失
        aux_loss = sum(
            layer.mlp.aux_loss
            for layer in self.layers
            if isinstance(layer.mlp, MOEFeedForward)
        ) # 如果没有使用MOE，则 aux_loss = sum([]) = 0

return hidden_states, presents, aux_loss
```

注意，回看MiniMind架构图，到现在为止，我们搭建的网络仅到RMSNorm层，后面的Linear和SoftMax还没有添加。

接下来需要进一步封装一个MiniMindForCausalLM类，这是为了更好地应用该模型于**因果语言建模任务（Causal Language Modeling）**，并增强其在推理、训练、生成等任务中的灵活性与兼容性。

因为虽然MiniMindModel已经实现了Transformer主干（包括嵌入层、注意力模块等核心组件），它只负责将输入的token ID编码为hidden states，属于“纯 backbone”模块。

而MiniMindForCausalLM是一个“任务级封装”，它在主干模型基础上加上了输出层（language modeling head，lm_head）和统一的输出结构，用于直接进行token-level的预测。

```python
from transformers import PreTrainedModel, GenerationMixin, PretrainedConfig
from transformers.modeling_outputs import CausalLMOutputWithPast

# MiniMindConfig='' # 仅占位

class MiniMindForCausalLM(PreTrainedModel, GenerationMixin):
    # config_class = MiniMindConfig

def __init__(self, config: MiniMindConfig = None):
        self.config = config or MiniMindConfig()
        super().__init__(self.config)

# 模型主干：MiniMindModel，输出 hidden_states
        self.model = MiniMindModel(self.config)

# 输出层：将 hidden_size 映射为 vocab_size（即每个 token 的 logits）
        self.lm_head = nn.Linear(self.config.hidden_size, self.config.vocab_size, bias=False)

# 权重绑定：embedding 权重与 lm_head 权重共享
        self.model.embed_tokens.weight = self.lm_head.weight

# 输出容器（CausalLMOutputWithPast 结构体，方便 structured return）
        self.OUT = CausalLMOutputWithPast()

def forward(self,
                input_ids: Optional[torch.Tensor] = None,                     # [batch_size, seq_len]
                attention_mask: Optional[torch.Tensor] = None,               # [batch_size, seq_len]
                past_key_values: Optional[List[Tuple[torch.Tensor, torch.Tensor]]] = None,
                use_cache: bool = True,
                logits_to_keep: Union[int, torch.Tensor] = 0,                # 控制 logits 保留哪些 token，一般训练时设置为0，推理时设置为1
                **args):

# 调用主干模型，输出 hidden_states、presents（KV缓存）、aux_loss
        h, past_kvs, aux_loss = self.model(
            input_ids=input_ids,                                            # 输入 token 序列
            attention_mask=attention_mask,                                  # 用于 mask padding 的 attention mask
            past_key_values=past_key_values,                                # 用于增量推理的 KV 缓存
            use_cache=use_cache,                                            # 是否返回 KV cache
            **args
        )
        # h.shape: [batch_size, total_seq_len, hidden_size]， 训练时，total_seq_len就是seq_len
        # past_kvs: List of (key, value), 每个层各一对
        # aux_loss: 用于 MOE 模型的辅助损失（如果使用MOE）

# 根据 logits_to_keep 参数决定保留输出的哪些位置
        slice_indices = slice(-logits_to_keep, None) if isinstance(logits_to_keep, int) else logits_to_keep

# 从 h 中保留最后 logits_to_keep 个位置，送入 lm_head 做分类
        logits = self.lm_head(h[:, slice_indices, :]) # 训练时，slice_indices 是 0，logits 相当于 self.lm_head(h[:, 0:, :])，即整个 h
        # logits.shape: [batch_size, logits_to_keep, vocab_size]

# 构建结构化输出字典
        self.OUT.__setitem__('last_hidden_state', h)          # [batch_size, seq_len, hidden_size]
        self.OUT.__setitem__('logits', logits)                # [batch_size, logits_to_keep, vocab_size]
        self.OUT.__setitem__('aux_loss', aux_loss)            # scalar or tensor
        self.OUT.__setitem__('past_key_values', past_kvs)     # list of tuples: (key, value)

return self.OUT
```

为了能够无缝对接HuggingFace的训练、推理与生成框架，MiniMindForCausalLM继承了`PreTrainedModel`和`GenerationMixin`，并使用标准的输出结构`CausalLMOutputWithPast`，从而实现了以下兼容性：

* 与`transformers.Trainer`配合训练时自动识别`logits`和`loss`;
* 支持`.generate()`方法进行文本生成（增量推理、KV缓存、温度采样等）;
* 与`LLaMA`、`GPT`等结构保持一致，便于迁移预训练权重或微调脚本;
* 通过`past_key_values`的接口设计，MiniMindForCausalLM 支持增量推理场景下的KV缓存机制，显著提升生成速度.

也就是说，通过这些兼容性，后续的许多代码不需要再次手动实现，而是可以直接调用HuggingFace官方实现的接口，方便快捷且高效。

```mermaid
flowchart TD
    %% 输入部分
    A[Input IDs: [B, T]] --> B[Token Embedding (B, T, hidden_size)]
    B --> C[Dropout Layer]

%% Transformer Stack
    C --> D0[MiniMindBlock Layer 0]
    D0 --> D1[MiniMindBlock Layer 1]
    D1 --> D2[MiniMindBlock Layer 2]
    D2 --> D3[...]
    D3 --> DN[MiniMindBlock Layer N-1]

%% MiniMindBlock 内部结构
    subgraph "MiniMindBlock"
        direction TB
        M1[Input RMSNorm] --> M2[Self-Attention + RoPE]
        M2 --> M3[Residual Add]
        M3 --> M4[Post-Attention RMSNorm]
        
        %% 条件分支
        M4 --> MD{Use MoE?}
        MD -->|No| M5[FeedForward (MLP)]
        MD -->|Yes| M6[MoEFeedForward (Sparse Experts)]
        M5 --> M7[Residual Add]
        M6 --> M7[Residual Add]
    end

%% 输出部分
    DN --> E[RMSNorm Layer]
    E --> F[Hidden States: [B, T, hidden_size]]
    F --> G[LM Head Linear Layer (B, T, vocab_size)]
    G --> H[Logits: [B, T, vocab_size]]
    H --> OUT[CausalLMOutputWithPast
    last_hidden_state, logits, aux_loss, past_key_values]

```

# 8.
当调用搭建好的`MiniMindForCausalLM`类实例化一个模型之后，模型的参数是随机的，这个阶段的模型没有任何语言能力，无法进行有意义的文本生成或理解。

**预训练**使用大规模的无监督语料对模型进行训练，使其具备“理解和生成自然语言”的基础能力，为后续的**微调**提供一个好的起点。

# 一、查看预训练数据集格式

MiniMind预训练使用的数据集为`pretrain_hq.jsonl`，这是一个1.55GB的文件，里面包含了非常多条数据，这里查看其中的第一条数据作为示例：

```python
import json
pretrain_dataset_path=r'D:\MyFile\github\minimind-master\minimind_dataset\pretrain_hq.jsonl'
with open(pretrain_dataset_path, 'r', encoding='utf-8') as f:
    for line_num, line in enumerate(f, 1):
        data = json.loads(line.strip())
        break
        
print(data.keys()) # dict_keys(['text'])
print(data)
```

```
{'text': '<|im_start|>鉴别一组中文文章的风格和特点，例如官方、口语、文言等。需要提供样例文章才能准确鉴别不同的风格和特点。<|im_end|> <|im_start|>好的，现在帮我查一下今天的天气怎么样?今天的天气依据地区而异。请问你需要我帮你查询哪个地区的天气呢？<|im_end|> <|im_start|>打开闹钟功能，定一个明天早上七点的闹钟。好的，我已经帮您打开闹钟功能，闹钟将在明天早上七点准时响起。<|im_end|> <|im_start|>为以下场景写一句话描述：一个孤独的老人坐在公园长椅上看着远处。一位孤独的老人坐在公园长椅上凝视远方。<|im_end|> <|im_start|>非常感谢你的回答。请告诉我，这些数据是关于什么主题的？这些数据是关于不同年龄段的男女人口比例分布的。<|im_end|> <|im_start|>帮我想一个有趣的标题。这个挺有趣的："如何成为一名成功的魔术师" 调皮的标题往往会吸引读者的注意力。<|im_end|> <|im_start|>回答一个问题，地球的半径是多少？地球的平均半径约为6371公里，这是地球自赤道到两极的距离的平均值。<|im_end|> <|im_start|>识别文本中的语气，并将其分类为喜悦、悲伤、惊异等。\n文本：“今天是我的生日！”这个文本的语气是喜悦。<|im_end|>'}
```

可以看到，每一条数据都是一个字典格式，只包含一个键值对，key是固定的'text'，value是用于预训练的“一段文本”，这是一个以 
`<|im_start|>`和`<|im_end|>`为对话边界token的多轮指令-回答对话数据集片段。

# 二、准备预训练数据加载器

构建符合PyTorch的Dataloader的Dataset类：

```python
import json
import torch
from torch.utils.data import Dataset

class PretrainDataset(Dataset):
    def __init__(self, data_path, tokenizer, max_length=512):
        super().__init__()
        self.tokenizer = tokenizer      # 分词器，用于将文本转为token ID
        self.max_length = max_length    # 每条样本的最大token长度
        self.samples = self.load_data(data_path)  # 加载数据

def load_data(self, path):
        """从文件中加载数据，每一行为一条JSON格式的样本"""
        samples = []
        with open(path, 'r', encoding='utf-8') as f:
            for line_num, line in enumerate(f, 1):
                # 读取每一行，解析成字典结构
                data = json.loads(line.strip())
                samples.append(data)
        return samples

def __len__(self):
        """返回样本数量"""
        return len(self.samples)

def __getitem__(self, index):
        """
        返回第 index 个样本：
        - X: 模型输入（input_ids[:-1]）
        - Y: 目标输出（input_ids[1:]）
        - loss_mask: 哪些token位置参与loss计算（去除padding部分）
        """
        sample = self.samples[index]

# 将样本中的文本字段进行tokenize
        encoding = self.tokenizer(
            str(sample['text']),                 # 转为字符串（确保数据类型一致）
            max_length=self.max_length,          # 限制最大长度
            padding='max_length',                # 不足部分补pad
            truncation=True,                     # 超出部分截断
            return_tensors='pt'                  # 返回PyTorch tensor形式（包含batch维度）
        )

# 获取input_ids张量，并去除batch维度（变成一维）
        input_ids = encoding.input_ids.squeeze()  # shape: [max_length]
        
        # 计算loss_mask：pad的位置不参与loss
        loss_mask = (input_ids != self.tokenizer.pad_token_id)  # shape: [max_length]，bool类型

# 语言模型是自回归的，使用前一个token预测下一个
        X = torch.tensor(input_ids[:-1], dtype=torch.long)         # 输入：[0, ..., n-2]
        Y = torch.tensor(input_ids[1:], dtype=torch.long)          # 目标：[1, ..., n-1]
        loss_mask = torch.tensor(loss_mask[1:], dtype=torch.long)  # loss_mask对齐目标Y

return X, Y, loss_mask
```

构建数据加载器：

```python
from torch.utils.data import DataLoader
from transformers import AutoTokenizer

max_length=512
data_path=r'D:\MyFile\github\minimind-master\minimind_dataset\pretrain_hq.jsonl'
tokenizer = AutoTokenizer.from_pretrained(r'D:\MyFile\github\minimind-master\model')
train_ds = PretrainDataset(data_path, tokenizer, max_length)

train_loader = DataLoader(
    train_ds,
    batch_size=2,
    pin_memory=True,
    drop_last=False,
    shuffle=False,
    num_workers=0,
)
```

查看数据总量以及数据的维度信息：

```python
print(len(train_loader)) # 706552
for item in train_loader:
    print([i.shape for i in item]) # [torch.Size([2, 511]), torch.Size([2, 511]), torch.Size([2, 511])]
    break
```

通过打印看到，数据总量为706552，每一条数据都包含3个PyTorch Tensor，分别是X, Y以及Y对应的padding mask（用于掩掉padding token的loss），shape都是`2x511`，2是batch_size，511是max_length-1，因为X和Y是正好是偏移一位的。

# 三、开始预训练

预训练代码和常规的模型训练代码几乎没有区别，核心代码段如下：

```python
# 定义交叉熵损失函数（不做reduction，保留每个token位置的loss）
loss_fct = nn.CrossEntropyLoss(reduction='none')

# CPU 不支持 float16 加速计算
ctx = nullcontext() if device_type == "cpu" else torch.cuda.amp.autocast()

# 遍历训练数据加载器
for step, (X, Y, loss_mask) in enumerate(train_loader):
    # print(step)  # 可用于调试

# 将数据转移到目标设备（如GPU）
    X = X.to(args.device)             # 输入 token 序列，形状: [batch_size, seq_len]
    Y = Y.to(args.device)             # 目标 token 序列，形状: [batch_size, seq_len]
    loss_mask = loss_mask.to(args.device)  # 用于遮蔽padding位置，形状: [batch_size, seq_len]

# 使用自定义学习率调度函数更新学习率
    lr = get_lr(
        epoch * iter_per_epoch + step,                # 当前训练步数（全局step）
        args.epochs * iter_per_epoch,                 # 总训练步数
        args.learning_rate                            # 初始学习率
    )
    for param_group in optimizer.param_groups:
        param_group['lr'] = lr                        # 动态更新优化器中的学习率

# 自动混合精度上下文（提高训练速度，降低显存）
    with ctx:  # ctx = autocast() 之类
        res = model(X)  # 前向传播，res.logits: [batch, seq_len, vocab_size]

# 计算token级别的交叉熵损失（不做平均）
        loss = loss_fct(
            res.logits.view(-1, res.logits.size(-1)),  # 转为2D: [batch*seq_len, vocab_size]
            Y.view(-1)                                 # 展平目标: [batch*seq_len]
        ).view(Y.size())  # reshape回[batch, seq_len]

# 仅在非pad的位置计算损失（通过loss_mask筛选）
        loss = (loss * loss_mask).sum() / loss_mask.sum()  # 平均有效token上的loss

# 加入模型可能返回的辅助损失（如正则项等）
        loss += res.aux_loss

# 梯度累积：将loss缩小为1/N，以模拟更大的batch
        loss = loss / args.accumulation_steps

# 使用GradScaler进行反向传播，支持AMP混合精度
    scaler.scale(loss).backward()

# 累积一定步数后才进行一次参数更新
    if (step + 1) % args.accumulation_steps == 0:
        # 取消scale，准备裁剪梯度（clip操作要求原始梯度）
        scaler.unscale_(optimizer)

# 裁剪梯度，防止爆炸
        torch.nn.utils.clip_grad_norm_(model.parameters(), args.grad_clip)

# 执行优化器步进
        scaler.step(optimizer)

# 更新scaler内部状态
        scaler.update()

# 清空梯度，准备下一次累计
        optimizer.zero_grad(set_to_none=True)
```
# 9.
# 一、查看有监督微调数据集格式

```python
import json
pretrain_dataset_path=r'D:\MyFile\github\minimind-master\minimind_dataset\sft_mini_512.jsonl'
with open(pretrain_dataset_path, 'r', encoding='utf-8') as f:
    for line_num, line in enumerate(f, 1):
        data = json.loads(line.strip())
        break
        
print(data.keys()) # dict_keys(['text'])
print(data)
```

```
{
    'conversations': 
    [
        {
            'role': 'user', 'content': '请告诉我在中国古代的“四大发明”是什么？'
        },
        {
            'role': 'assistant', 'content': '中国古代的“四大发明”是指造纸术、印刷术、火药和指南针。这四项发明对世界文明的发展产生了深远的影响：\n\n1. **造纸术**：据史书记载，东汉时期的蔡伦改进了造纸工艺，使得纸张的生产更加便捷、成本更低，质量也更加优良。这一发明极大地促进了文化的传播和保存。\n\n2. **印刷术**：中国古代的印刷术最早可以追溯到唐代的雕版印刷，到了宋代发展出了活字印刷技术。印刷术的发明极大地促进了知识的传播，降低了书籍的成本，对教育和文化的发展起到了重要的推动作用。\n\n3. **火药**：火药最初是在唐代被发现的，最初可能用于医疗或炼金术。到了宋代，人们开始将火药用于军事目的，发明了各种火器。火药的发明改变了战争的面貌，对世界军事技术的发展产生了重大影响。\n\n4. **指南针**：指南针最初在中国被用于风水测量，后来逐渐发展成为航海导航的重要工具。这一发明极大地促进了海上航行技术的发展，对于新航路的开辟和世界地理大发现起到了关键作用。\n\n这四项发明不仅在中国历史上占有重要地位，而且对全世界的科技进步和文明发展都产生了深远的影响。'
        }
    ]
}
```

# 二、准备有监督微调数据加载器

构建符合PyTorch的Dataloader的Dataset类：

```python
import json
import torch
from torch.utils.data import Dataset

class SFTDataset(Dataset):
    def __init__(self, jsonl_path, tokenizer, max_length=1024):
        super().__init__()
        self.tokenizer = tokenizer                  # 分词器
        self.max_length = max_length                # 最大输入长度（会进行截断或填充）
        self.samples = self.load_data(jsonl_path)   # 加载数据样本
        self.bos_id = tokenizer('<|im_start|>assistant', add_special_tokens=False).input_ids# [1, 1078, 538, 501]， [1]是<|im_start|>这个特殊token的id，[1078, 538, 501]是assistant的分词id
        self.eos_id = tokenizer('<|im_end|>', add_special_tokens=False).input_ids# [2]

def __len__(self):
        return len(self.samples)  # 返回样本数量

def load_data(self, path):
        """从 jsonl 文件加载对话数据"""
        samples = []
        with open(path, 'r', encoding='utf-8') as f:
            for line_num, line in enumerate(f, 1):
                data = json.loads(line.strip())  # 每行为一个 JSON 对象
                samples.append(data)
        return samples

def _create_chat_prompt(self, conversations):
        """
        将对话轮构造成符合 ChatML 格式的字符串：
        每一轮用户/助手对话被标注为 'user' / 'assistant'
        最终用 tokenizer 的 apply_chat_template 统一构造 prompt。
        """
        messages = []
        for i, turn in enumerate(conversations):
            role = 'user' if i % 2 == 0 else 'assistant'  # 偶数轮为用户，奇数轮为助手
            messages.append({"role": role, "content": turn['content']})

# 返回字符串形式的 prompt，而非直接 tokenize
        return self.tokenizer.apply_chat_template(
            messages,
            tokenize=False,
            add_generation_prompt=False
        )

def _generate_loss_mask(self, input_ids):
        """
        构建损失掩码，只有 assistant 的回答部分才参与 loss 计算。
        找出每一段 assistant 的响应，在其 <|im_start|>assistant 和 <|im_end|> 之间设置 loss_mask 为 1。
        """
        loss_mask = [0] * len(input_ids)
        i = 0
        while i < len(input_ids):
            # 找 assistant 开头标志
            if input_ids[i:i + len(self.bos_id)] == self.bos_id:
                start = i + len(self.bos_id)  # 答案起点
                end = start
                while end < len(input_ids):
                    # 查找 assistant 的回答终止符 <|im_end|>
                    if input_ids[end:end + len(self.eos_id)] == self.eos_id:
                        break
                    end += 1
                # 为 assistant 回答部分（从 start + 1 到 end 之间）设置 loss mask
                for j in range(start + 1, min(end + len(self.eos_id) + 1, self.max_length)):
                    loss_mask[j] = 1
                # 跳过到下一个 segment
                i = end + len(self.eos_id) if end < len(input_ids) else len(input_ids)
            else:
                i += 1
        return loss_mask

def __getitem__(self, index):
        sample = self.samples[index]

# 构建 ChatML 格式 prompt（字符串）
        prompt = self._create_chat_prompt(sample['conversations'])

# 分词并截断，确保长度 <= max_length
        input_ids = self.tokenizer(prompt).input_ids[:self.max_length]

# 右侧填充 pad_token 直到 max_length 长度
        input_ids += [self.tokenizer.pad_token_id] * (self.max_length - len(input_ids))

# 生成动态 loss mask，仅对 assistant 响应位置计算 loss
        loss_mask = self._generate_loss_mask(input_ids)

# 构建训练样本：
        # 模型输入为前 n-1 个 token，预测目标为第 2 到第 n 个 token
        X = torch.tensor(input_ids[:-1], dtype=torch.long)         # 输入序列
        Y = torch.tensor(input_ids[1:], dtype=torch.long)          # 目标标签（shifted）
        loss_mask = torch.tensor(loss_mask[1:], dtype=torch.long)  # 对齐 Y 的位置（从第一个预测 token 开始）

return X, Y, loss_mask
```

沿着`__getitem__`方法，逐行向下解析。

## 2.1 `sample = self.samples[index]`

`sample = self.samples[index]`用于获取self.samples中对应index的一条数据，这是从原始`.jsonl`数据集中读取的，如上所述，它只有一个key叫做`conversations`，取出其value，示例如下：

```
[
    {
        'role': 'user', 'content': '请告诉我在中国古代的“四大发明”是什么？'
    }, 
    
    {
        'role': 'assistant', 'content': '中国古代的“四大发明”是指造纸术、印刷术、火药和指南针。这四项发明对世界文明的发展产生了深远的影响：\n\n1. **造纸术**：据史书记载，东汉时期的蔡伦改进了造纸工艺，使得纸张的生产更加便捷、成本更低，质量也更加优良。这一发明极大地促进了文化的传播和保存。\n\n2. **印刷术**：中国古代的印刷术最早可以追溯到唐代的雕版印刷，到了宋代发展出了活字印刷技术。印刷术的发明极大地促进了知识的传播，降低了书籍的成本，对教育和文化的发展起到了重要的推动作用。\n\n3. **火药**：火药最初是在唐代被发现的，最初可能用于医疗或炼金术。到了宋代，人们开始将火药用于军事目的，发明了各种火器。火药的发明改变了战争的面貌，对世界军事技术的发展产生了重大影响。\n\n4. **指南针**：指南针最初在中国被用于风水测量，后来逐渐发展成为航海导航的重要工具。这一发明极大地促进了海上航行技术的发展，对于新航路的开辟和世界地理大发现起到了关键作用。\n\n这四项发明不仅在中国历史上占有重要地位，而且对全世界的科技进步和文明发展都产生了深远的影响。'
    }
]
```

## 2.2 `prompt = self._create_chat_prompt(sample['conversations'])`

`self._create_chat_prompt(sample['conversations'])`将上述sample应用一种称之为ChatML的模板，它是一种专门为多轮对话任务设计的Prompt模板格式，用于格式化输入，模板如下：

```matlab
{% for message in messages %}
<|im_start|>{{ message['role'] }}
{{ message['content'] }}<|im_end|>
{% endfor %}
```

上述代码使用了`self.tokenizer.apply_chat_template`方法来应用ChatML模板，其中tokenize=False表示只返回字符串形式的prompt，不进行分词。add_generation_prompt=False表示是否在最后自动添加`<|im_start|>assistant`这样的生成提示，用于推理阶段.如果是训练数据（已经包括答案），一般设为 False。

应用ChatML模板后得到的prompt为：

```
'<|im_start|>system\nYou are a helpful assistant<|im_end|>\n<|im_start|>user\n请告诉我在中国古代的“四大发明”是什么？<|im_end|>\n<|im_start|>assistant\n中国古代的“四大发明”是指造纸术、印刷术、火药和指南针。这四项发明对世界文明的发展产生了深远的影响：\n\n1. **造纸术**：据史书记载，东汉时期的蔡伦改进了造纸工艺，使得纸张的生产更加便捷、成本更低，质量也更加优良。这一发明极大地促进了文化的传播和保存。\n\n2. **印刷术**：中国古代的印刷术最早可以追溯到唐代的雕版印刷，到了宋代发展出了活字印刷技术。印刷术的发明极大地促进了知识的传播，降低了书籍的成本，对教育和文化的发展起到了重要的推动作用。\n\n3. **火药**：火药最初是在唐代被发现的，最初可能用于医疗或炼金术。到了宋代，人们开始将火药用于军事目的，发明了各种火器。火药的发明改变了战争的面貌，对世界军事技术的发展产生了重大影响。\n\n4. **指南针**：指南针最初在中国被用于风水测量，后来逐渐发展成为航海导航的重要工具。这一发明极大地促进了海上航行技术的发展，对于新航路的开辟和世界地理大发现起到了关键作用。\n\n这四项发明不仅在中国历史上占有重要地位，而且对全世界的科技进步和文明发展都产生了深远的影响。<|im_end|>\n'
```

紧接着对这个prompt使用tokenizer编码成input_ids，并根据最大序列长度进行padding处理。

## 2.3 loss_mask = self._generate_loss_mask(input_ids)

这里仅对assistant响应位置（也就是assistant回复的内容）计算loss，因此需要找出每一段assistant的响应，在其`<|im_start|>assistant`和`<|im_end|>`之间设置loss_mask为1，其余位置的loss_mask均为0。

使用`_generate_loss_mask`方法实现上述功能。

基本思想就是遍历整个input_ids，查找出现`<|im_start|>assistant`的位置start，这是模型回复开始的标志；然后继续遍历，找到第一个出现的`<|im_end|>`的位置end，start到end之间的计算模型的回复，loss_mask设置为1。

如果是多轮对话，就继续往后遍历，查找第二个模型预测开始的位置`<|im_start|>assistant`，以此类推。

最后，和预训练一样，返回X, Y以及Y对应的loss mask。

现在来构建数据加载器：

```python
from torch.utils.data import DataLoader
from transformers import AutoTokenizer

max_length=512
data_path=r'D:\MyFile\github\minimind-master\minimind_dataset\sft_mini_512.jsonl'
tokenizer = AutoTokenizer.from_pretrained(r'D:\MyFile\github\minimind-master\model')
train_ds = SFTDataset(data_path, tokenizer, max_length)

train_loader = DataLoader(
    train_ds,
    batch_size=2,
    pin_memory=True,
    drop_last=False,
    shuffle=False,
    num_workers=0,
)
```

查看一下有监督微调的数据总量以及数据的维度信息：

```python
print(len(train_loader)) # 607362
for item in train_loader:
    print([i.shape for i in item]) # [torch.Size([2, 511]), torch.Size([2, 511]), torch.Size([2, 511])]
    break
```

通过打印看到，有监督微调的数据总量为607362，每一条数据都包含3个PyTorch Tensor，分别是X, Y以及Y对应的padding mask（用于掩掉padding token的loss），shape都是`2x511`，2是batch_size，511是max_length-1，因为X和Y是正好是偏移一位的。这一点和预训练一样。

# 三、开始有监督微调

有监督微调代码和常规的模型预训练代码几乎没有区别，直接核心代码段粘贴过来：

```python
loss_fct = nn.CrossEntropyLoss(reduction='none')
for step, (X, Y, loss_mask) in enumerate(train_loader):
    X = X.to(args.device)
    Y = Y.to(args.device)
    loss_mask = loss_mask.to(args.device)
    lr = get_lr(epoch * iter_per_epoch + step, args.epochs * iter_per_epoch, args.learning_rate)
    for param_group in optimizer.param_groups:
        param_group['lr'] = lr

with ctx:
        res = model(X)
        loss = loss_fct(
            res.logits.view(-1, res.logits.size(-1)),
            Y.view(-1)
        ).view(Y.size())

loss = (loss * loss_mask).sum() / loss_mask.sum()
        loss += res.aux_loss
        loss = loss / args.accumulation_steps

scaler.scale(loss).backward()

if (step + 1) % args.accumulation_steps == 0:
        scaler.unscale_(optimizer)
        torch.nn.utils.clip_grad_norm_(model.parameters(), args.grad_clip)

scaler.step(optimizer)
        scaler.update()

optimizer.zero_grad(set_to_none=True)
```
# 10.
**DPO（Direct Preference Optimization）** 是一种用于有监督指令微调后模型偏好对齐的训练方法，目标是让模型更倾向于输出人类偏好的回答（`chosen`），而不是次优回答（`rejected`）。

# 一、查看DPO训练数据集格式

```python
import json
pretrain_dataset_path=r'D:\MyFile\github\minimind-master\minimind_dataset\dpo.jsonl'
with open(pretrain_dataset_path, 'r', encoding='utf-8') as f:
    for line_num, line in enumerate(f, 1):
        data = json.loads(line.strip())
        break
        
print(data.keys()) # dict_keys(['chosen', 'rejected'])
print(data)
```

```
{
    'chosen': 
        [
            {
                'content': 'How many moles of HBr are required to react ...', 
                'role': 'user'
            }, 
            
            {
                'content': 'To determine the number of moles of HBr ...',
            
                'role': 'assistant'
            }
        ],
        
    'rejected': 
        [
            {
                'content': 'How many moles of HBr are required to react ...',

'role': 'user'
            }, 
                
            {
                'content': 'To answer this question, we need to write  ...', 
            
                'role': 'assistant'
            }
        ]
}
```

用于DPO训练的数据集中，每一条是数据都包含至少两个assistant回答，一个优、一个劣，“chosen”对应优，“rejected”对应劣。

在DPO训练时，模型会学习让“chosen”回答的概率高于“rejected”回答，从而实现偏好对齐。

# 二、准备DPO训练数据加载器

构建符合PyTorch的Dataloader的Dataset类：

```python
import json
import torch
from torch.utils.data import Dataset

class DPODataset(Dataset):
    def __init__(self, file_path, tokenizer, max_length=4096):
        super().__init__()
        self.tokenizer = tokenizer
        self.max_length = max_length
        self.padding = tokenizer.pad_token_id if tokenizer.pad_token_id is not None else 0

# 加载 JSONL 格式数据：每行为一个 dict，有 chosen 和 rejected
        with open(file_path, 'r', encoding='utf-8') as f:
            self.data = []
            for line in f:
                line = line.strip()
                obj = json.loads(line)
                self.data.append(obj)

def __len__(self):
        return len(self.data)

def __getitem__(self, index):
        item = self.data[index]

chosen = item['chosen']
        rejected = item['rejected']

# 拼接成字符串（不 tokenize，只生成 prompt 文本）
        chosen_prompt = self.tokenizer.apply_chat_template(
            chosen, tokenize=False, add_generation_prompt=False
        )
        rejected_prompt = self.tokenizer.apply_chat_template(
            rejected, tokenize=False, add_generation_prompt=False
        )

# 编码为 input_ids（截断 + 填充）
        chosen_encoding = self.tokenizer(
            chosen_prompt,
            truncation=True,
            max_length=self.max_length,
            padding='max_length'
        )
        rejected_encoding = self.tokenizer(
            rejected_prompt,
            truncation=True,
            max_length=self.max_length,
            padding='max_length'
        )

# 转换为 token ID 列表，长度为 max_length
        chosen_input_ids = chosen_encoding['input_ids']           # shape: (max_length,)
        rejected_input_ids = rejected_encoding['input_ids']       # shape: (max_length,)

# 构造 loss mask：仅在 assistant 段落（<|im_start|>assistant ... <|im_end|>）中的 token 参与损失
        chosen_loss_mask = self._generate_loss_mask(chosen_input_ids)     # shape: (max_length,)
        rejected_loss_mask = self._generate_loss_mask(rejected_input_ids) # shape: (max_length,)

# （MiniMind没有将padding的token掩掉）

# 构造训练数据：左移一位预测（即 y 是 x 的下一位）
        x_chosen = torch.tensor(chosen_input_ids[:-1], dtype=torch.long)      # shape: (max_length - 1,)
        y_chosen = torch.tensor(chosen_input_ids[1:], dtype=torch.long)       # shape: (max_length - 1,)
        mask_chosen = torch.tensor(chosen_loss_mask[1:], dtype=torch.long)    # shape: (max_length - 1,)

x_rejected = torch.tensor(rejected_input_ids[:-1], dtype=torch.long)  # shape: (max_length - 1,)
        y_rejected = torch.tensor(rejected_input_ids[1:], dtype=torch.long)   # shape: (max_length - 1,)
        mask_rejected = torch.tensor(rejected_loss_mask[1:], dtype=torch.long)# shape: (max_length - 1,)

return {
            'x_chosen': x_chosen,           # shape: (max_length - 1,)
            'y_chosen': y_chosen,           # shape: (max_length - 1,)
            'mask_chosen': mask_chosen,     # shape: (max_length - 1,)

'x_rejected': x_rejected,       # shape: (max_length - 1,)
            'y_rejected': y_rejected,       # shape: (max_length - 1,)
            'mask_rejected': mask_rejected  # shape: (max_length - 1,)
        }

def _generate_loss_mask(self, input_ids):
        """
        根据 <|im_start|>assistant 和 <|im_end|> 的位置标记哪些 token 应该参与损失计算。
        返回一个和 input_ids 等长的 0/1 mask。
        """
        loss_mask = [0] * len(input_ids)
        i = 0
        while i < len(input_ids):
            # 匹配一个 assistant 段落开头
            if input_ids[i:i + len(self.bos_id)] == self.bos_id:
                start = i + len(self.bos_id)
                end = start
                while end < len(input_ids):
                    # 查找 assistant 的回答终止符 <|im_end|>
                    if input_ids[end:end + len(self.eos_id)] == self.eos_id:
                        break
                    end += 1
                # 在 <|im_start|>assistant 和 <|im_end|> 之间部分启用 loss
                for j in range(start + 1, min(end + len(self.eos_id) + 1, self.max_length)):
                    loss_mask[j] = 1
                i = end + len(self.eos_id) if end < len(input_ids) else len(input_ids)
            else:
                i += 1
        return loss_mask
```

`DPODataset`和之前的`SFTDataset`的处理逻辑是完全一致的，只不过`DPODataset`中需要处理两次(chosen和rejected)，因此上述代码中包含的函数介绍可以去看`SFTDataset`，这里不再重复介绍。

# 三、DPO 损失函数

DPO的目标是让训练后模型更偏好人类认为更好的答案（chosen），而不是差的答案（rejected），并且这种偏好是在对比参考模型(refrence model)的基础上学来的。

这里的参考模型，一般指的是微调前的模型，比如做了预训练和SFT之后的模型。

参考：https://allam.vercel.app/post/dpo/

DPO旨在以一种更简单、更稳定的方式替代传统RLHF中复杂的奖励建模过程。它的核心在于：使用一个直接可微的损失函数，来优化模型对人类偏好的响应倾向，而无需训练单独的奖励模型或使用复杂的强化学习方法（如PPO）。

具体来说，DPO在一对偏好样本上进行优化：它增加人类偏好响应中token的对数概率，同时减少非偏好响应中的对数概率，从而促使模型产生更符合人类意图的输出。

从数学角度看，这一过程相当于为模型引入了一个隐式奖励函数，该函数通过log-ratio的差值衡量当前策略相对于参考策略对人类偏好的一致程度，并直接用于梯度优化。

设：

- $\pi$ 是当前模型（policy model）
- $\pi_\text{ref}$ 是参考模型（reference model）
- $x$ 是输入 prompt
- $y^+$ 是人类偏好的回答（`chosen`）
- $y^-$ 是次优回答（`rejected`）
- $\beta$ 是温度超参（调节梯度幅度）

DPO loss 如下：

$$
\mathcal{L}_{\text{DPO}} = \mathbb{E}_{(x, y^+, y^-) \sim \mathcal{D}} \left[ -\log \sigma \left( \beta \cdot \left( \log \frac{\pi(y^+|x)}{\pi_{\text{ref}}(y^+|x)} - \log \frac{\pi(y^-|x)}{\pi_{\text{ref}}(y^-|x)} \right) \right) \right]
$$

其中 $\sigma$ 是 sigmoid 函数。

在上述公式的log差值项中，前一个表示模型对于人类偏好`chosen`回复$y^+$的对数概率，后一个表示模型对于`rejected`回复$y^-$的对数概率，DPO loss的目标是最大化两者的差值，也就是鼓励模型$\pi$相较于$\pi_\text{ref}$更加偏好$y^+$而非$y^-$。其中除以$\pi_\text{ref}$的作用是作为一个正则化因子，确保训练后的模型过度偏离原始模型。

在MiniMind的代码实现中，根据对数运算的性质，调换了DPO loss中的对数项顺序，如下：
$$
\mathcal{L}_{\text{DPO}} = \mathbb{E}_{(x, y^+, y^-) \sim \mathcal{D}} \left[ -\log \sigma \left( \beta \cdot \left( \log \frac{\pi(y^+|x)}{\pi(y^-|x)} - \log \frac{\pi_{\text{ref}}(y^+|x)}{\pi_{\text{ref}}(y^-|x)} \right) \right) \right]
$$

代码实现上述DPO loss：

```python
def dpo_loss(ref_probs, probs, mask, beta):
    # ref_probs: (batch_size, seq_len) 来自参考模型（Reference Model）的 log-probs
    # probs: (batch_size, seq_len)     来自当前策略模型（Policy Model）的 log-probs
    # mask: (batch_size, seq_len)      用于标记哪些 token 被计入损失（如生成部分）
    # beta: float                      DPO 的超参数控制分布偏移强度

# Step 1: 每个样本的有效长度（非 padding 部分 token 的数量）
    seq_lengths = mask.sum(dim=1, keepdim=True)  # (batch_size, 1)

# Step 2: 对每个样本计算平均 log-probs，仅在 mask == 1 的位置有效
    ref_probs = (ref_probs * mask).sum(dim=1) / seq_lengths.squeeze(1)  # (batch_size,)
    probs = (probs * mask).sum(dim=1) / seq_lengths.squeeze(1)          # (batch_size,)

# Step 3: 将 batch 划分为前一半为 chosen，后一半为 rejected
    batch_size = ref_probs.shape[0]  # 假设 batch_size 是偶数，前半是 chosen，后半是 rejected

chosen_ref_probs = ref_probs[:batch_size // 2]     # (batch_size // 2,)
    reject_ref_probs = ref_probs[batch_size // 2:]     # (batch_size // 2,)
    chosen_probs = probs[:batch_size // 2]             # (batch_size // 2,)
    reject_probs = probs[batch_size // 2:]             # (batch_size // 2,)

# Step 4: log-ratio 比较（策略模型 vs 参考模型）
    pi_logratios = chosen_probs - reject_probs         # (batch_size // 2,)
    ref_logratios = chosen_ref_probs - reject_ref_probs  # (batch_size // 2,)

# Step 5: DPO 损失计算，鼓励 chosen 比 rejected 的分数更高
    logits = pi_logratios - ref_logratios              # (batch_size // 2,)
    loss = -F.logsigmoid(beta * logits)                # (batch_size // 2,)

return loss.mean()  # 标量，.mean()等价于DPO loss数学公式中的期望符号E
```

在Step 3中，之所以取batch的前后一半分别作为chosen和rejected，是因为在MiniMind的train函数中，为了并行执行训练，对chosen和rejected做了拼接（在数据加载器中做了padding，因此可以拼接），相应的代码在下一节展示。

```
一句话速通：
把同一 prompt 的两条回答（chosen / rejected）分别过一遍参考模型和当前模型，算出 log-prob 后取平均，再用 sigmoid 让 chosen 的相对分高过 rejected，最后用 -log 当损失，就这么简单。
30 秒拆解：
先算每条序列的真实长度（mask 加和）。
把 log-prob 按有效长度取平均，消除 token 数差异。
把 batch 劈成两半：前半 chosen，后半 rejected。
拿当前模型算 “chosen 比 rejected 好多少”（pi_logratios），再减去参考模型的同样差值（ref_logratios），得到 logits。
用 β·logits 送进 sigmoid，再取负对数，平均就是损失。
核心直觉：
如果当前模型让 chosen 比 rejected 的相对提升（相对参考模型）越大，sigmoid 输出越接近 1，损失越接近 0；反之则损失爆炸，反向传播逼模型往 chosen 方向改。
```

# 四、开始训练DPO

训练DPO的代码在SFT训练代码的基础上，将交叉熵损失换成了DPO loss，如下：

```python
for step, batch in enumerate(train_loader):

# x_chosen: (batch_size, seq_len)
    x_chosen = batch['x_chosen'].to(args.device)

# x_rejected: (batch_size, seq_len)
    x_rejected = batch['x_rejected'].to(args.device)

# 标签 token ids（通常是 x 向右 shift 一位）
    # y_chosen: (batch_size, seq_len)
    y_chosen = batch['y_chosen'].to(args.device)

# y_rejected: (batch_size, seq_len)
    y_rejected = batch['y_rejected'].to(args.device)

# mask_chosen: (batch_size, seq_len)，mask 表示哪些位置计算 loss（只在 assistant 回复部分）
    mask_chosen = batch['mask_chosen'].to(args.device)

# mask_rejected: (batch_size, seq_len)
    mask_rejected = batch['mask_rejected'].to(args.device)

# 拼接成整体 batch（大小为 2B）
    # x: (2 * batch_size, seq_len)
    x = torch.cat([x_chosen, x_rejected], dim=0)
    y = torch.cat([y_chosen, y_rejected], dim=0)
    mask = torch.cat([mask_chosen, mask_rejected], dim=0)

# 设置学习率
    lr = get_lr(epoch * iter_per_epoch + step, args.epochs * iter_per_epoch, args.learning_rate)
    for param_group in optimizer.param_groups:
        param_group['lr'] = lr

with ctx:  # mixed precision/autocast 上下文
        with torch.no_grad():  # 冻结参考模型（ref_model）参数
            # ref_logits: (2 * batch_size, seq_len, vocab_size)
            ref_outputs = ref_model(x)
            ref_logits = ref_outputs.logits

# 参考模型的 log prob，对应标签 token 的概率
        # ref_probs: (2 * batch_size, seq_len)
        ref_probs = logits_to_probs(ref_logits, y)
        ref_probs = ref_probs * mask  # 掩盖非 assistant 区域

# 当前模型 logits
        # logits: (2 * batch_size, seq_len, vocab_size)
        outputs = model(x)
        logits = outputs.logits

# 当前模型的 token-level log prob
        # probs: (2 * batch_size, seq_len)
        probs = logits_to_probs(logits, y)
        probs = probs * mask

# 计算 DPO 损失（内部比较 probs[:batch_size] 与 probs[batch_size:]）
        loss = dpo_loss(ref_probs, probs, mask, beta=0.1)

# 梯度累积处理
        loss = loss / args.accumulation_steps

# 反向传播（混合精度）
    scaler.scale(loss).backward()

# 累积完成后更新参数
    if (step + 1) % args.accumulation_steps == 0:
        scaler.unscale_(optimizer)
        torch.nn.utils.clip_grad_norm_(model.parameters(), args.grad_clip)
        scaler.step(optimizer)
        scaler.update()
        optimizer.zero_grad(set_to_none=True)
```

```
把 chosen 回答和 rejected 回答各复制一份，拼成一条双倍长度的 batch。
让“冻结的老模型”和“正在训练的新模型”分别给每个 token 打分，只保留助手回答部分的分数。
算个简单的对比损失：让新模型给 chosen 的分数比 rejected 高就行；其它全是工程细节（混合精度、梯度累积）用来省显存、防爆炸。
如果你现在只想做一件事：
把 beta 先设 0.1，跑通流程；loss 下降就说明方向对了，剩下参数慢慢调。
```

上述代码中有一个函数`logits_to_probs`，可以将输入的logits(shape为[2 x batch_size, seq_len, vocab_size])转换成输出的对数概率probs（shape为[2 x batch_size, seq_len]），其定义如下：

```python
def logits_to_probs(logits, labels):
    # logits: Tensor of shape (batch_size, seq_len, vocab_size)
    # labels: Tensor of shape (batch_size, seq_len)

# Step 1: 计算每个 token 的 log-softmax 概率
    log_probs = F.log_softmax(logits, dim=2)  
    # log_probs: (batch_size, seq_len, vocab_size)

# Step 2: 收集 labels 对应的 log 概率
    # labels.unsqueeze(2): (batch_size, seq_len, 1)
    # torch.gather(..., dim=2): 从 log_probs 的第3维（vocab_size）中选择对应 label 的概率
    probs = torch.gather(log_probs, dim=2, index=labels.unsqueeze(2))  
    # probs: (batch_size, seq_len, 1)

probs = probs.squeeze(-1)  
    # probs: (batch_size, seq_len)  => 每个 token 的 log-probability

return probs
```

输入的`logits`表示模型在该位置预测下一个token是词表中某个词的原始分数，shape为[batch_size, seq_len, vocab_size]。

第一步，将`logits`使用log_softmax转换为对数概率`log_probs`，即`log_probs`表示模型在该位置预测下一个token是词表中某个词的对数概率，shape不变。

第二步，通过torch.gather，从`log_probs`中查询输入的真实标签`labels`中每个token对应位置的log概率，shape为[batch_size, seq_len]，这是每个位置上真实标签的模型预测对数概率，也就是DPO loss的输入。

```
一句话：把“模型对每个位置所有词预测的 logits”变成“模型对正确答案（labels）给出的 log-probability”。
```

# 11.
# 一、LoRA的核心思想

LoRA，全称 **Low-Rank Adaptation of Large Language Models**，是一种在 **大模型中进行高效微调** 的方法，目标是 **只训练极少数参数** 就能让模型适应新任务，避免重新训练整个大模型，从而可以在没有充足GPU显存的情况下快速在自己的数据集上对大模型做微调。

![](https://miro.medium.com/v2/resize:fit:720/format:webp/1*XdoGFaSME49GrqfBPGJqdQ.png)

在Transformer、ViT、GPT等模型中，很多计算都包含线性层：
$$y = W x$$

$$
W \in \mathbb{R}^{d_{\text{out}} \times d_{\text{in}}}
$$

LoRA 的做法是：**不直接更新大模型参数W**，而是在其旁边**插入一个低秩矩阵BA**，作为可训练的残差项：
$$y = W x + BAx$$

其中：
$$ A \in \mathbb{R}^{r \times d_{\text{in}}} $$
$$ B \in \mathbb{R}^{d_{\text{out}} \times r} $$
$$ r \ll d_{\text{in}}, d_{\text{out}} $$

原先微调需要更新整个$W$，其参数量为$\text{Param}(W) = d_{\text{out}} \times d_{\text{in}}$，使用LoRA后，$B A$的参数量仅为$\text{Param}_{\text{LoRA}} = r \times d_{\text{in}} + d_{\text{out}} \times r = r (d_{\text{in}} + d_{\text{out}})$

使用PyTorch实现LoRA类，如下：

```python
# 定义Lora网络结构
class LoRA(nn.Module):
    def __init__(self, in_features, out_features, rank):
        super().__init__()
        self.rank = rank  # LoRA的秩（rank），控制低秩矩阵的大小
        self.A = nn.Linear(in_features, rank, bias=False)  # 低秩矩阵A
        self.B = nn.Linear(rank, out_features, bias=False)  # 低秩矩阵B
        # 矩阵A高斯初始化
        self.A.weight.data.normal_(mean=0.0, std=0.02)
        # 矩阵B全0初始化
        self.B.weight.data.zero_()

def forward(self, x):
        return self.B(self.A(x))
```

# 二、如何将LoRA注入到现有的LLM中？

下面的代码实现了这一功能：

```python
def apply_lora(model, rank=16):
    for name, module in model.named_modules():

if isinstance(module, nn.Linear) and module.weight.shape[0] == module.weight.shape[1]:
            # 如果是 nn.Linear 且为方阵，则插入 LoRA 模块
            lora = LoRA(module.weight.shape[0], module.weight.shape[1], rank=rank).to(model.device)
            setattr(module, "lora", lora)  # 给 module 加一个 lora 成员变量
            original_forward = module.forward  # 保存原始 forward 方法

# 构造新 forward：原始输出 + LoRA 输出
            def forward_with_lora(x, layer1=original_forward, layer2=lora):
                return layer1(x) + layer2(x)

module.forward = forward_with_lora  # 替换 forward 方法
```

举个简单模型的例子：

```python
# 测试模型
class TestModel(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = nn.Linear(1024, 1024)  # 方阵线性层

@property
    def device(self):
        return next(self.parameters()).device  # 返回模型参数所在设备

def forward(self, x):
        return self.linear(x)

model = TestModel()
print(model)
```

打印原始模型的结构：

```
TestModel(
  (linear): Linear(in_features=1024, out_features=1024, bias=True)
)
```

这表明TestModel有一个成员变量linear，是一个标准的nn.Linear层

注入LoRA：

```python
apply_lora(model)
print(model)
```

打印注入LoRA后的model：

```
TestModel(
  (linear): Linear(
    in_features=1024, out_features=1024, bias=True
    (lora): LoRA(
      (A): Linear(in_features=1024, out_features=16, bias=False)
      (B): Linear(in_features=16, out_features=1024, bias=False)
    )
  )
)
```

可以看到，lora层已经成功注入。

lora模块被注入到了nn.Linear中，成为nn.Linear这个module的一个成员变量。

我们可以打印模型的每一层：

```python
for name, module in model.named_modules():
    print(f"{name}: {module.__class__.__name__}")
```

```
: TestModel
linear: Linear
linear.lora: LoRA
linear.lora.A: Linear
linear.lora.B: Linear
```

# 三、LoRA权重的加载与保存

因为训练时只更新LoRA的参数，因此在保存和加载模型权重时，只需要处理更新的这部分LoRA参数。

首先，注入lora的model为：

递归遍历打印模型中的所有模块：

```python
for name, module in model.named_modules():
    print(name,':',module)
```

如下：

```
: TestModel(
  (linear): Linear(
    in_features=1024, out_features=1024, bias=True
    (lora): LoRA(
      (A): Linear(in_features=1024, out_features=16, bias=False)
      (B): Linear(in_features=16, out_features=1024, bias=False)
    )
  )
)
linear : Linear(
  in_features=1024, out_features=1024, bias=True
  (lora): LoRA(
    (A): Linear(in_features=1024, out_features=16, bias=False)
    (B): Linear(in_features=16, out_features=1024, bias=False)
  )
)
linear.lora : LoRA(
  (A): Linear(in_features=1024, out_features=16, bias=False)
  (B): Linear(in_features=16, out_features=1024, bias=False)
)
linear.lora.A : Linear(in_features=1024, out_features=16, bias=False)
linear.lora.B : Linear(in_features=16, out_features=1024, bias=False)
```

可以看到，总共5个子模块。

我们只关心拥有`lora`属性的模块：

```python
# for name, module in model.named_modules():
#     attrs = [attr for attr in dir(module) if not attr.startswith('__')]
#     if 'lora' in attrs:
#         print(name,"------",module)
for name, module in model.named_modules():
    if hasattr(module, 'lora'):
        print(name,"------",module)
```

输出：

```
linear ------ Linear(
  in_features=1024, out_features=1024, bias=True
  (lora): LoRA(
    (A): Linear(in_features=1024, out_features=16, bias=False)
    (B): Linear(in_features=16, out_features=1024, bias=False)
  )
)
```

可以看到，只有第二个子模块`linear`具有`lora`属性，在模型训练时，也只有这一层的参数会被更新。

因此我们只需要保存`linear.lora`层的权重即可：

```python
def save_lora(model, path):
    state_dict = {}
    for name, module in model.named_modules():
        if hasattr(module, 'lora'):
            for k, v in module.lora.state_dict().items():
                state_dict[f"{name}.lora.{k}"] = v
    torch.save(state_dict, path)
    print(f"[LoRA] Saved {len(state_dict)} params to: {path}")

save_lora(model, "lora.pth")
```

加载保存的"lora.pth"，并解析其结构：

```python
lora = torch.load("lora.pth")
for k, v in lora.items():
    print(k, v.shape)
```

```
linear.lora.A.weight torch.Size([16, 1024])
linear.lora.B.weight torch.Size([1024, 16])
```

相应地，在加载训练好的模型权重时，也只是加载lora层的权重：

```python
def load_lora(model, path):
    state_dict = torch.load(path, map_location=model.device)
    for name, module in model.named_modules():
        if hasattr(module, 'lora'):
            # replace用于隐掉{name}.lora.，因为load的执行者是module.lora.，不去掉会重复
            lora_state = {k.replace(f'{name}.lora.', ''): v for k, v in state_dict.items() if f'{name}.lora.' in k}
            # 调试信息
            for k, v in lora_state.items():
                print(k,'----',v.shape)
            print(module.lora)
            module.lora.load_state_dict(lora_state)
```

```python
load_lora(model, "lora.pth")
```

加载时的调试输出信息：

```
A.weight ---- torch.Size([16, 1024])
B.weight ---- torch.Size([1024, 16])
LoRA(
  (A): Linear(in_features=1024, out_features=16, bias=False)
  (B): Linear(in_features=16, out_features=1024, bias=False)
)
```

# 四、训练LoRA

这里将lora注入到MIniMind模型后，直接复用SFT的数据加载器和训练函数，相应的代码和SFT保持一致。

来看一下注入lora前后的训练参数量变化：

```python
# 初始化模型和分词器
model, tokenizer = init_model(lm_config)

# 注入 LoRA 模块（低秩适配器）
apply_lora(model)

# 计算总参数量
total_params = sum(p.numel() for p in model.parameters())

# 计算所有带有 "lora" 名字的参数量（即 LoRA 层的参数）
lora_params_count = sum(p.numel() for name, p in model.named_parameters() if 'lora' in name)

# 只在主进程中打印参数信息（DDP 分布式时）
if not ddp or dist.get_rank() == 0:
    print(f"LLM 总参数量: {total_params}")
    print(f"LoRA 参数量: {lora_params_count}")
    print(f"LoRA 参数占比: {lora_params_count / total_params * 100:.2f}%")

# 冻结除 LoRA 外的所有参数，只训练 LoRA 层
for name, param in model.named_parameters():
    if 'lora' not in name:
        param.requires_grad = False

# 收集 LoRA 可训练参数
lora_params = []
for name, param in model.named_parameters():
    if 'lora' in name:
        lora_params.append(param)

# 构建优化器，仅优化 LoRA 参数
optimizer = optim.AdamW(lora_params, lr=args.learning_rate)

# 构建数据集，这里复用SFT的数据加载器
train_ds = SFTDataset(args.data_path, tokenizer, max_length=args.max_seq_len)

# 如果使用分布式训练（DDP），使用 DistributedSampler 划分数据
train_sampler = DistributedSampler(train_ds) if ddp else None

# 构建数据加载器
train_loader = DataLoader(
    train_ds,
    batch_size=args.batch_size,
    pin_memory=True,
    drop_last=False,
    shuffle=False,  # 如果用 DDP，不能设置 shuffle
    num_workers=args.num_workers,
    sampler=train_sampler
)

# 使用自动混合精度（AMP），加速训练、节省显存，仅当使用 float16 或 bfloat16 时启用
scaler = torch.cuda.amp.GradScaler(enabled=(args.dtype in ['float16', 'bfloat16']))

# 每个 epoch 的迭代次数
iter_per_epoch = len(train_loader)

# 开始训练多个 epoch
for epoch in range(args.epochs):
    train_epoch(epoch, wandb)  # 执行单轮训练，wandb 可用于记录训练日志
```

输出：

```
LLM 总参数量: 26092032
LoRA 参数量: 262144
LoRA 参数占比: 1.00%
```
# 12.

# 一、LoRA的核心思想